题目内容
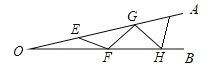
【题目】已知,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作
边上一点,作![]() ,分别交边
,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

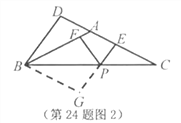
(1)若![]() (如图1),求证:
(如图1),求证:![]() .
.
(2)若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() .试猜想:线段
.试猜想:线段![]() ,
,![]() 和
和![]() 之间的数量关系,并就
之间的数量关系,并就![]() 情形(如图2)说明理由.
情形(如图2)说明理由.
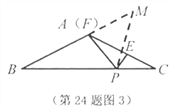
(3)若点![]() 与
与![]() 重合(如图3),
重合(如图3),![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②设![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .
.
【答案】(1)证明见解析;(2)猜想:![]() ,理由见解析;(3)①
,理由见解析;(3)①![]() ;②证明见解析.
;②证明见解析.
【解析】(1)根据平行线的判定,得到![]() ,
,![]() ,证明
,证明![]() .即可证明
.即可证明![]() .
.
(2)过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() ≌
≌![]() 得到
得到![]() .
.
证明四边形![]() 是平行四边形,即可得到
是平行四边形,即可得到![]() .
.
(3)①设![]() ,
,![]() ,根据三角形的内角和列出方程,求解即可.
,根据三角形的内角和列出方程,求解即可.
②延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,证明
,证明 ![]() .根据相似三角形的性质得到
.根据相似三角形的性质得到
![]() ,即可证明.
,即可证明.
【解答】(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
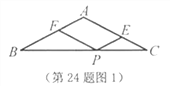
(2)猜想:![]() ,理由如下:
,理由如下:
过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ≌
≌![]() ∴
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
(3)①设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
②延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,
∵![]() ,
,![]() .
.
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目