题目内容
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C,(﹣1,﹣2),D(1,﹣2),点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为_____.
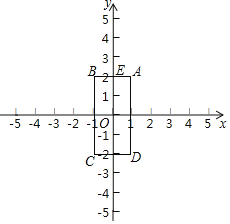
【答案】(﹣1,﹣1).
【解析】
由点A、B、C、D的坐标可得出AB、BC的长度,设点M和点N第2017次相遇时的时间为x,根据第一次相遇的路程和=周长,所以第2017次相遇的路程和=周长×2017,即可得出关于x的一元一次方程,解之即可得出x的值,再根据路程=速度×时间可求出M和点N第2017次相遇时,点M走过的路程,结合矩形的周长为12,即可找出点M和点N第2017次相遇时的坐标,此题得解.
解:∵A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2),
∴AB=2,BC=4.
设点M和点N第2017次相遇时的时间为x,
根据题意得:(1+2)x=2017×2×(4+2),
解得:x=8068,
∴M和点N第2017次相遇时,点M走过的路程为x=8068.
∵矩形ABCD的周长为12,8068=672×12+4,
∴M和点N第2017次相遇时的位置在距离点E逆时针方向的4个单位长度.
∵BC=4,BE=1,
∴点M和点N第2017次相遇时的位置为线段CF的中点,即点(﹣1,﹣1).
故答案为:(﹣1,﹣1).


练习册系列答案
相关题目