题目内容
【题目】如图,平面直角坐标系中A(0,a),B(b,0),且a、b满足![]() 作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.
作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.

(1)求点A、B的坐标;
(2)设△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)点M为线段OP的中点,连接AM,当点P在线段BA上时,△AOM的面积为△AOB面积的![]() 时,求出t值,并求出点M到x轴距离.
时,求出t值,并求出点M到x轴距离.
【答案】(1)A(0,6),B(﹣8,0);(2)S=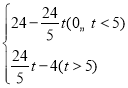 ;(3)t=
;(3)t=![]() ,点M到x轴距离为1.
,点M到x轴距离为1.
【解析】
(1)解二元一次方程组,即可得到A,B坐标;
(2)根据点P的位置,分点P在线段AB上和点P在线段BA延长线上进行讨论,作![]() ,使用
,使用![]() 的面积,进行等面积转化,求出
的面积,进行等面积转化,求出![]() 长度,表示出
长度,表示出![]() 长度,则
长度,则![]() ;
;
(3)由M为OP中点可知,![]() ,结合
,结合![]() ,推出
,推出![]() ,得到
,得到![]() ,求出运动时间t;由M为OP中点,得
,求出运动时间t;由M为OP中点,得![]() ,从而得到点M到
,从而得到点M到![]() 轴的距离.
轴的距离.
(1)由![]() ,解得
,解得![]() ,
,
∴A(0,6),B(﹣8,0).
(2)∵AB=10,
∴点P从B运动到A的时间为5秒,
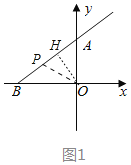
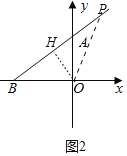
当0≤t<5时,如图1中,作OH⊥AB于H.
∵S△AOB=![]() OAOB=
OAOB=![]() ABOH,
ABOH,
∴OH=![]() =
=![]()
S=![]() PAOH=
PAOH=![]() (10﹣2t)×
(10﹣2t)×![]() =24﹣
=24﹣![]() t.
t.
当t>5时,S=![]() PAOH=
PAOH=![]() (2t﹣10)×
(2t﹣10)×![]() =
=![]() t﹣24.
t﹣24.
综上所述,S=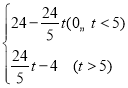 .
.
(3)如图3中,连接BM.
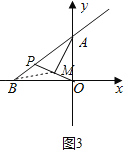
∵OM=PM,
∴S△AOM=S△APM,
∵S△AOM=![]() S△AOB,
S△AOB,
∴S△OPB=![]() S△AOB,
S△AOB,
∴BP=![]() AB,
AB,
∴2t=![]() ,
,
∴t=![]() ,
,
设点M到x轴的距离为h.
∵OM=PM,
∴S△OBM=![]() S△OPB=
S△OPB=![]() S△AOB,
S△AOB,
∴![]() ×8×h=
×8×h=![]() ×
×![]() ×6×8,
×6×8,
解得h=1,
∴点M到x轴距离为1.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中甲、乙两组学生人数都为6人,成绩如下(单位:分):
甲:7,9,10,8,5,9;
乙:9,6,8,10,7,8
(1)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | |
甲组 | 8 | 9 | ||
乙组 |
| 8 | 8 |
(2)甲组学生说他们的众数高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出一条支持乙组学生观点的理由. .