ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΘ®1Θ©Έ ΧβΖΔœ÷
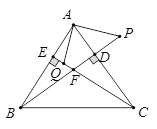
»γΆΦΔΌΘ§÷±œΏABΓΈCDΘ§E «AB”κAD÷°ΦδΒΡ“ΜΒψΘ§Ν§Ϋ”BEΘ§CEΘ§Ω…“‘ΖΔœ÷ΓœB+ΓœCΘΫΓœBECΘ°

«κΑ―œ¬ΟφΒΡ÷ΛΟςΙΐ≥Χ≤Ι≥δΆξ’ϊΘΚ
÷ΛΟςΘΚΙΐΒψEΉςEFΓΈABΘ§
ΓΏABΓΈDCΘ®“―÷ΣΘ©Θ§EFΓΈABΘ®Η®÷ζœΏΒΡΉςΖ®Θ©Θ§
ΓύEFΓΈDCΘ®ΓΓ ΓΓΘ©
ΓύΓœCΘΫΓœCEFΘ°Θ®ΓΓ ΓΓΘ©
ΓΏEFΓΈABΘ§ΓύΓœBΘΫΓœBEFΘ®Ά§άμΘ©Θ§
ΓύΓœB+ΓœCΘΫΓΓ ΓΓΘ®Β»ΝΩ¥ζΜΜΘ©
Φ¥ΓœB+ΓœCΘΫΓœBECΘ°
Θ®2Θ©ΆΊ’ΙΧΫΨΩ
»γΙϊΒψE‘ΥΕ·ΒΫΆΦΔΎΥυ ΨΒΡΈΜ÷ΟΘ§ΤδΥϊΧθΦΰ≤Μ±δΘ§«σ÷ΛΘΚΓœB+ΓœCΘΫ360Γψ©¹ΓœBECΘ°
Θ®3Θ©ΫβΨωΈ Χβ
»γΆΦΔέΘ§ABΓΈDCΘ§ΓœCΘΫ120ΓψΘ§ΓœAECΘΫ80ΓψΘ§‘ρΓœAΘΫΓΓ ΓΓΘ°Θ®÷°Φδ–¥≥ωΫα¬έΘ§≤Μ”Ο–¥ΦΤΥψΙΐ≥ΧΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΤΫ––”ΎΆ§“Μ÷±œΏΒΡΝΫ÷±œΏΤΫ––Θ§ΝΫ÷±œΏΤΫ––Θ§ΡΎ¥μΫ«œύΒ»Θ§ΓœBEF+ΓœCEFΘΜΘ®2Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©20ΓψΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψ![]() Ής
Ής![]() Θ§ΗυΨίΤΫ––œΏΒΡ≈–Ε®ΒΟ≥ω
Θ§ΗυΨίΤΫ––œΏΒΡ≈–Ε®ΒΟ≥ω![]() Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΦ¥Ω…ΘΜ
Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΦ¥Ω…ΘΜ
Θ®2Θ©ΙΐΒψ![]() Ής
Ής![]() Θ§ΗυΨίΤΫ––œΏΒΡ≈–Ε®ΒΟ≥ω
Θ§ΗυΨίΤΫ––œΏΒΡ≈–Ε®ΒΟ≥ω![]() Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΦ¥Ω…ΘΜ
Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΦ¥Ω…ΘΜ
Θ®3Θ©ΙΐΒψ![]() Ής
Ής![]() Θ§ΗυΨίΤΫ––œΏΒΡ≈–Ε®ΒΟ≥ω
Θ§ΗυΨίΤΫ––œΏΒΡ≈–Ε®ΒΟ≥ω![]() Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΦ¥Ω…Θ°
Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΦ¥Ω…Θ°
Θ®1Θ©÷ΛΟςΘΚ»γΆΦΔΌΘ§ΙΐΒψEΉςEFΓΈABΘ§
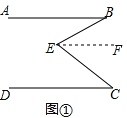
ΓΏABΓΈDCΘ®“―÷ΣΘ©Θ§EFΓΈABΘ®Η®÷ζœΏΒΡΉςΖ®Θ©Θ§
ΓύEFΓΈDCΘ®ΤΫ––”ΎΆ§“Μ÷±œΏΒΡΝΫ÷±œΏΤΫ––Θ©Θ§
ΓύΓœCΘΫΓœCEFΘ°Θ®ΝΫ÷±œΏΤΫ––Θ§ΡΎ¥μΫ«œύΒ»Θ©Θ§
ÿEFøABȧ
ΓύΓœBΘΫΓœBEFΘ®Ά§άμΘ©Θ§
ΓύΓœB+ΓœCΘΫΓœBEF+ΓœCEFΘ®Β»ΝΩ¥ζΜΜΘ©
Φ¥ΓœB+ΓœCΘΫΓœBECΘ§
Ι ¥πΑΗΈΣΘΚΤΫ––”ΎΆ§“Μ÷±œΏΒΡΝΫ÷±œΏΤΫ––Θ§ΝΫ÷±œΏΤΫ––Θ§ΡΎ¥μΫ«œύΒ»Θ§ΓœBEF+ΓœCEFΘΜ
Θ®2Θ©÷ΛΟςΘΚ»γΆΦΔΎΘ§ΙΐΒψEΉςEFΓΈABΘ§
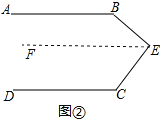
ΓΏABΓΈDCΘ®“―÷ΣΘ©Θ§EFΓΈABΘ®Η®÷ζœΏΒΡΉςΖ®Θ©Θ§
ΓύEFΓΈDCΘ®ΤΫ––”ΎΆ§“Μ÷±œΏΒΡΝΫ÷±œΏΤΫ––Θ©Θ§
ΓύΓœC+ΓœCEFΘΫ180ΓψΘ§ΓœB+ΓœBEFΘΫ180ΓψΘ§
ΓύΓœB+ΓœC+ΓœAECΘΫ360ΓψΘ§
ΓύΓœB+ΓœCΘΫ360Γψ©¹ΓœBECΘΜ
Θ®3Θ©ΫβΘΚ»γΆΦΔέΘ§ΙΐΒψEΉςEFΓΈABΘ§

ΓΏABΓΈDCΘ®“―÷ΣΘ©Θ§EFΓΈABΘ®Η®÷ζœΏΒΡΉςΖ®Θ©Θ§
ΓύEFΓΈDCΘ®ΤΫ––”ΎΆ§“Μ÷±œΏΒΡΝΫ÷±œΏΤΫ––Θ©Θ§
ΓύΓœC+ΓœCEFΘΫ180ΓψΘ§ΓœAΘΫΓœBEFΘ§
ΓΏΓœCΘΫ120ΓψΘ§ΓœAECΘΫ80ΓψΘ§
ΓύΓœCEFΘΫ180Γψ©¹120ΓψΘΫ60ΓψΘ§
ΓύΓœBEFΘΫ80Γψ©¹60ΓψΘΫ20ΓψΘ§
ΓύΓœAΘΫΓœAEFΘΫ20ΓψΘ°
Ι ¥πΑΗΈΣΘΚ20ΓψΘ°