题目内容
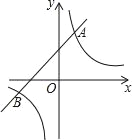
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
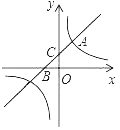
【答案】(1)y=![]() ;y=x+1;(2)P点的坐标为(3,0)或(﹣5,0).
;y=x+1;(2)P点的坐标为(3,0)或(﹣5,0).
【解析】
(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;
(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
解:(1)把A(1,2)代入双曲线y=![]() ,可得k=2,
,可得k=2,
∴双曲线的解析式为y=![]() ;
;
把A(1,2)代入直线y=x+b,可得b=1,
∴直线的解析式为y=x+1;
(2)设P点的坐标为(x,0),
在y=x+1中,令y=0,则x=﹣1;令x=0,则y=1,
∴B(﹣1,0),C(0,1),即BO=1=CO,
∵△BCP的面积等于2,
∴![]() BP×CO=2,即
BP×CO=2,即![]() |x﹣(﹣1)|×1=2,
|x﹣(﹣1)|×1=2,
解得x=3或﹣5,
∴P点的坐标为(3,0)或(﹣5,0).

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
【题目】“元旦”期间,某文具店购进 ![]() 只两种型号的文具进行销售,其进价和售价如表:
只两种型号的文具进行销售,其进价和售价如表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用 ![]() 元可以购进A,B两种型号的文具各多少只?
元可以购进A,B两种型号的文具各多少只?
(2)在(![]() )的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过
)的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过 ![]() ?请你说明理由.
?请你说明理由.
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?