Question

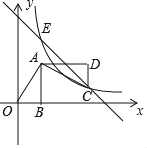
【题目】如图，平面直角坐标系中，OB在x轴上，∠ABO＝90°，点A的坐标为（1，2）．将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在双曲线y＝的一个分支上，过C点的直线y＝﹣x+b与双曲线的另一个交点为E，则△EOC的面积为_____．

Answer 1

【答案】4

【解析】

由旋转可得点D的坐标为（3，2），那么可得到点C的坐标为（3，1），代入即可求得双曲线的解析式，代入求出一次函数的解析式，联立双曲线的解析式求得交点E的坐标，再将不规则图形的面积转化为规则图形的面积计算即可．

平面直角坐标系中，OB在x轴上，∠ABO＝90°，点A的坐标为（1，2）．

由旋转可知D（3，2），C（3，1），

把C（3，1）代入y＝中，可得k＝3，

∴所求的双曲线的解析式为y＝，

把C（3，1）代入y＝﹣x+b中，得b＝4，

∴直线的解析式为y＝﹣x+4．

∴﹣x+4＝，

解得x1＝1，x2＝3，

∴E（1，3），

如图：

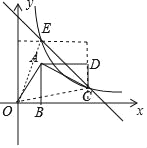
S△EOC＝3×3﹣×1×3﹣×3×1﹣×2×2＝4，

故答案为：4．