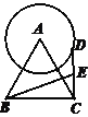题目内容
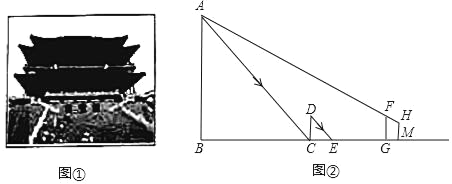
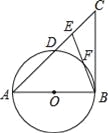
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求![]() 的长.
的长.

图1 图2
【答案】(1)BE="FH" ;理由见解析
(2)证明见解析
(3)![]() =2π
=2π
【解析】
试题(1)由△ABE≌△EHF(SAS)即可得到BE=FH
(2)由(1)可知AB=EH,而BC=AB,FH=EB,从而可知△FHC是等腰直角三角形,∠FCH为45°,而∠ACB也为45°,从而可证明
(3)由已知可知∠EAC=30°,AF是直径,设圆心为O,连接EO,过点E作EN⊥AC于点N,则可得△ECN为等腰直角三角形,从而可得EN的长,进而可得AE的长,得到半径,得到![]() 所对圆心角的度数,从而求得弧长
所对圆心角的度数,从而求得弧长
试题解析:(1)BE=FH。理由如下:
∵四边形ABCD是正方形 ∴∠B=90°,
∵FH⊥BC ∴∠FHE=90°
又∵∠AEF=90° ∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°
∴∠HEF=∠BAE ∴ ∠AEB=∠EFH 又∵AE=EF
∴△ABE≌△EHF(SAS)
∴BE=FH
(2)∵△ABE≌△EHF
∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE="CH"
∴CH=FH
∴∠FCH=45°,∴∠FCM=45°
∵AC是正方形对角线,∴ ∠ACD=45°
∴∠ACF=∠FCM +∠ACD =90°
(3)∵AE=EF,∴△AEF是等腰直角三角形
△AEF外接圆的圆心在斜边AF的中点上。设该中点为O。连结EO得∠AOE=90°

过E作EN⊥AC于点N
Rt△ENC中,EC=4,∠ECA=45°,∴EN=NC=![]()
Rt△ENA中,EN =![]()
又∵∠EAF=45° ∠CAF=∠CEF=15°(等弧对等角)
∴∠EAC=30°
∴AE=![]()
Rt△AFE中,AE=![]() = EF,∴AF=8
= EF,∴AF=8
AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°
![]() =2π·4·(90°÷360°)=2π
=2π·4·(90°÷360°)=2π

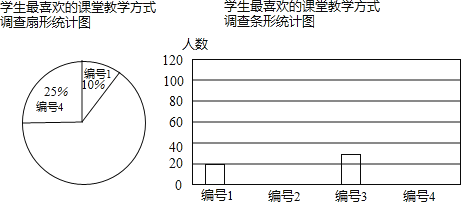
【题目】某中学为促进课堂教学,提高教学质量,对九年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
(1)请把三个图表中的空缺部分都补充完整;
(2)你最喜欢以上哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由(字数在20字以内).
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | 0.5 | |
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
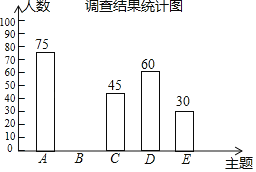
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.