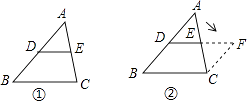题目内容
【题目】如图,ABCD中,AB=13,AD=10,将ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( ) 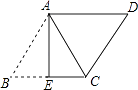
A.5
B.12
C.3
D.![]()
【答案】B
【解析】解:∵翻折后点B恰好与点C重合,
∴AE⊥BC,BE=CE,
∵BC=AD=10,
∴BE=5,
∴AE= ![]() =12,
=12,
∵AD∥BC,
∴点C到AD的距离=AE,
故点C到AD的距离是12,
故选B.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.

练习册系列答案
相关题目
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |
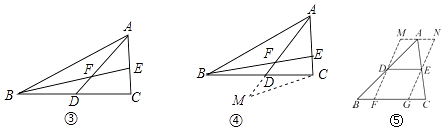

请你利用小亮的发现解决下列问题:
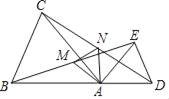
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .