题目内容
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.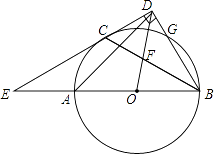
(1)求证:CD是⊙O的切线.
(2)若 ![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ![]() ,求AD的长.
,求AD的长.
【答案】
(1)证明:如图1,连接OC,AC,CG,
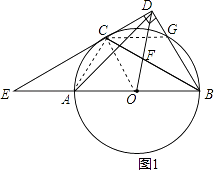
∵AC=CG,
∴ ![]() ,
,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线
(2)解:∵OC∥BD,
∴△OCF∽△BDF,△EOC∽△EBD,
∴ ![]() ,
,
∴ ![]() ,
,
∵OA=OB,
∴AE=OA=OB,
∴OC= ![]() OE,
OE,
∵∠ECO=90°,
∴∠E=30°
(3)解:如图2,过A作AH⊥DE于H,
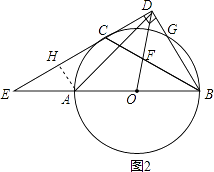
∵∠E=30°
∴∠EBD=60°,
∴∠CBD= ![]() EBD=30°,
EBD=30°,
∵CD= ![]() ,
,
∴BD=3,DE=3 ![]() ,BE=6,
,BE=6,
∴AE= ![]() BE=2,
BE=2,
∴AH=1,
∴EH= ![]() ,
,
∴DH=2 ![]() ,
,
在Rt△DAH中,AD= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连接OC,AC,CG,由圆周角定理,得出∠ABC=∠CBG,再根据同圆的半径相等机等量代换求得∠OCB=∠CBG,根据平行线的判定得到OC∥BG,由已知CD⊥BG,得出OC⊥CD,即可证得结论。
(2)由OC∥BD,得出△OCF∽△BDF,△EOC∽△EBD,得出对应边成比例,再根据直角三角形的性质,可求出∠E的度数。
(3)过A作AH⊥DE于H,通过解直角三角形求出BD、BE、DE的长,在Rt△DAH中,根据勾股定理求出AD的长。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目