Question

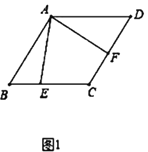
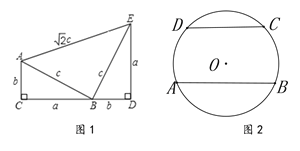
【题目】如图1，四边形ACDE是美国第二十任总统伽菲尔德验证勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE=，这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”．

请解决下列问题：

（1）判断方程是否是 “勾系一元二次方程”；并说明理由．

（2）求证：关于的“勾系一元二次方程” 必有实数根；

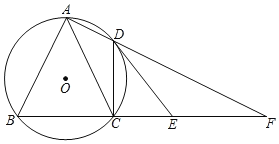
（3）如图2，已知AB、CD是半径为5的⊙O的两条平行弦，AB=2a，CD=2b，a≠b，关于x的方程是“勾系一元二次方程”，求∠BAC的度数

Answer 1

【答案】（1）是，理由详见解析；（2）详见解析；（3）45°

【解析】

（1）根据“勾系一元二次方程”的定义即可判断；

（2）利用勾股定理以及“勾系一元二次方程”的定义即可解决问题；

（3）如图2中，连接OC，OB，作OE⊥CD于E，作EO的延长线交AB于F，利用全等三角形的性质推导出∠COB=90°即可解决问题．

（1）是 “勾系一元二次方程”，理由如下：

∵中，

∴

∴，能构成直角三角形

∴方程是“勾系一元二次方程”

（2）∵关于的方程是“勾系一元二次方程”

∴构成直角三角形，c是斜边

∴

∵

∴

∴关于的“勾系一元二次方程”必有实数根．

（3）在图2中，连接OC，OB，作OE⊥CD于E，作EO的延长线交AB于F，如下图：

∵关于x的方程是“勾系一元二次方程”

∴，5构成直角三角形，5是斜边

∴

∵AB//CD，OE⊥CD

∴OF⊥AB

∴∠OEC=∠OFB= 90°

∴

∵AB=2a，CD=2b

∴

∵，

∴

∴

∴

∴

∵

∴

∴

∴