题目内容
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AB=AC,CE=10,EF=14,求CD.
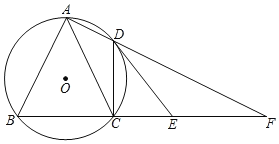
【答案】(1)证明见解析;(2)CD=![]() .
.
【解析】
(1)连接BD,由直径所对的圆周角是![]() 可知∠BCD=90°,结合三角形外角的性质及同弧所对的圆周角相等可得∠BDC+∠CDE=90°,由切线的判定定理可证结论;
可知∠BCD=90°,结合三角形外角的性质及同弧所对的圆周角相等可得∠BDC+∠CDE=90°,由切线的判定定理可证结论;
(2)由∠BAF=∠BDE=90°可得∠F+∠ABC=∠FDE+∠ADB,由等腰三角形两底角相等的性质及同弧所对的圆周角相等,等量代换可得∠F=∠FDE,易知DE长,由勾股定理可求得CD长.
解:(1)如图,连接BD.
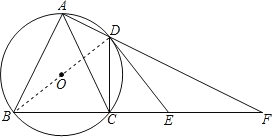
∵∠BAD=90°,
∴点O必在BD上,即:BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°.
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°.
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠BAF=∠BDE=90°,
∴∠F+∠ABC=∠FDE+∠ADB=90°.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ADB=∠ACB,
∴∠ABC=∠ADB,
∴∠F=∠FDE,
∴DE=EF=14.
∵CE=10,∠BCD=90°,
∴∠DCE=90°,
∴CD=![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】(数据收集)
以下是从某校九年级男生中随机选出的10名男生,分别测量了他们的身高(单位:cm),数据整理如下:
163 171 173 159 161 174 164 166 169 164
(数据分析)
确定这十个数据的众数、中位数、平均数,并填入表.
众数 | 中位数 | 平均数 |
|
|
|
(得出结论)
(1)若用样本中的统计量估计该校九年级男生平均身高,则这个统计量是 ;(选填“众数”或“中位数”或“平均数”中一个)
(2)若该校九年级共有男生280名,选用合适的统计量估计,该校九年级男生身高超过平均身高的人数.
【题目】二次函数y=ax2+bx+c的x,y的部分对应值如表所示,则下列判断不正确的是( )
x | ﹣2 | ﹣1 | 0 | 1 | 2 |
y | ﹣2.5 | 0 | 1.5 | 2 | 1.5 |
A.当x<0时,y随x的增大而增大
B.对称轴是直线x=1
C.当x=4时,y=﹣2
D.方程ax2+bx+c=0有一个根是3
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A、B城往C、D两乡运肥料的平均费用如下表. 现C乡需要肥料240吨,D乡需要肥料260吨.
A城(出) | B城(出) | |
C乡(人) | 20元/吨 | 15元/吨 |
D乡(人) | 25元/吨 | 30元/吨 |
(1)A城和B城各多少吨肥料?
(2)设从B城运往D乡肥料x吨,总运费为y元,求y与x之间的函数关系,并写出自变量x的取值范围;
(3)由于更换车型,使B城运往D乡的运费每吨减少a元(a>0),其余路线运费不变,若C、D两乡的总运费最小值不少于10040元,求a的最大整数值.