题目内容
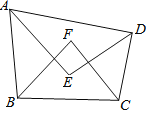
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. 
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC﹣∠CBF=∠EBF﹣∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有  ,
,
∴△ABF≌△CBE(SAS)
(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°﹣∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°,
∴△CEF是直角三角形.
【解析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB=135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.本题考查了正方形的性质.全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)根据判定定理SAS证明△ABF≌△CBE;(2)通过角的计算得出∠CEF=90°.本题属于中档题,难度不大,解决该题型题目时,通过正方形和等腰三角形的性质找出相等的边,再通过角的计算找出相等的角,以此来证明两三角形全等是关键.