题目内容
【题目】如图,AB=AC,AD=AE,BE、CE相交于点F,则图中全等三角形共有( )对.

A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
先依据等边对等角的性质得到∠ABC=∠ACB,然后再结合全等三角形的判定定理进行判断即可.
连接BC,
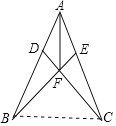
∵AB=AC,AD=AE,
∴∠ABC=∠ACB,BD=EC,
∵在△BDC和△CEB中,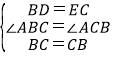 ,
,
∴△BDC≌△CEB(SAS),
∴∠EBC=∠DCB,
∴∠ABF=∠ACF,
在△DBF和△ECF中,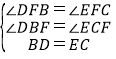 ,
,
∴△DBF≌△ECF(AAS),
∵∠EBC=∠DCB,
∴FB=FC,
∵在△ABF和△ACF中,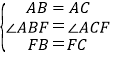 ,
,
∴△ABF≌△ACF(SAS),
∴∠DAF=∠EAF,
∵在△DAF和△EAF中,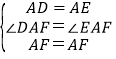 ,
,
∴△DAF≌△EAF(SAS),
∵在△DAC和△EAB中,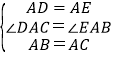 ,
,
∴△DAC≌△EAB(SAS).
故选:C.

练习册系列答案
相关题目





