题目内容
【题目】如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上. 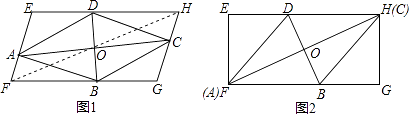
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知 ![]() =2,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
=2,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
【答案】
(1)证明:∵点O是菱形ABCD对角线AC、BD的交点,
∴OA=OC,OD=OB,
∵点O是线段FH的中点,
∴OF=OH.
在△AOF和△COH中,有  ,
,
∴△AOF≌△COH(SAS),
∴∠AFO=∠CHO,
∴AF∥CH.
同理可得:DH∥BF.
∴四边形EFGH是平行四边形
(2)设矩形EFGH的长为a、宽为b,则AC= ![]() .
.
∵ ![]() =2,
=2,
∴BD= ![]() AC=
AC= ![]() ,OB=
,OB= ![]() BD=
BD= ![]() ,OA=
,OA= ![]() AC=
AC= ![]() .
.
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOB=90°.
∵四边形EFGH是矩形,
∴∠AGH=90°,
∴∠AOB=∠AGH=90°,
又∵∠BAO=∠CAG,
∴△BAO∽△CAG,
∴ ![]() ,即
,即 ![]() ,
,
解得:a=2b①.
∵S菱形ABCD= ![]() ACBD=
ACBD= ![]()
![]()
![]() =20,
=20,
∴a2+b2=80②.
联立①②得: ![]() ,
,
解得: ![]() ,或
,或 ![]() (舍去).
(舍去).
∴矩形EFGH的长为8,宽为4
【解析】(1)根据菱形的性质可得出OA=OC,OD=OB,再由中点的性质可得出OF=OH,结合对顶角相等即可利用全等三角形的判定定理(SAS)证出△AOF≌△COH,从而得出AF∥CH,同理可得出DH∥BF,依据平行四边形的判定定理即可证出结论;(2)设矩形EFGH的长为a、宽为b.根据勾股定理及边之间的关系可找出AC= ![]() ,BD=
,BD= ![]() ,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出
,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出 ![]() ,套入数据即可得出a=2b①,再根据菱形的面积公式得出a2+b2=80②,联立①②解方程组即可得出结论.本题考查了平行四边形的判定、全等三角形的判定及性质、菱形的性质、矩形的性质以及相似三角形的判定及性质,解题的关键:(1)找出AF∥CH、DH∥BF;(2)找出关于a、b的二元二次方程组.本题属于中档题,难度不大,但解题过程叫繁琐,解决该题型题目时,根据相似三角形的性质找出对应边的比例关系是关键.
,套入数据即可得出a=2b①,再根据菱形的面积公式得出a2+b2=80②,联立①②解方程组即可得出结论.本题考查了平行四边形的判定、全等三角形的判定及性质、菱形的性质、矩形的性质以及相似三角形的判定及性质,解题的关键:(1)找出AF∥CH、DH∥BF;(2)找出关于a、b的二元二次方程组.本题属于中档题,难度不大,但解题过程叫繁琐,解决该题型题目时,根据相似三角形的性质找出对应边的比例关系是关键.







