题目内容
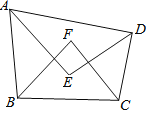
【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.
【答案】(1)220;110;(2)∠E+∠F=180°.理由见解析;(3)AB∥CD.
【解析】试题分析:(1)先根据三角形内角和定理求出∠FBC+∠BCF=180°-∠F=110°,再由角平分线定义得出∠ABC=2∠FBC,∠BCD=2∠BCF,那么∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=220°;由四边形ABCD的内角和为360°,得出∠BAD+∠CDA=360°-(∠ABC+∠BCD)=140°.由角平分线定义得出∠DAE=![]() ∠BAD,∠ADE=
∠BAD,∠ADE=![]() ∠CDA,那么∠DAE+∠ADE=
∠CDA,那么∠DAE+∠ADE=![]() ∠BAD+
∠BAD+![]() ∠CDA=
∠CDA=![]() (∠BAD+∠CDA)=70°,然后根据三角形内角和定理求出∠E=180°-(∠DAE+∠ADE)=110°;
(∠BAD+∠CDA)=70°,然后根据三角形内角和定理求出∠E=180°-(∠DAE+∠ADE)=110°;
(2)由四边形ABCD的内角和为360°得到∠BAD+∠CDA+∠ABC+∠BCD=360°,由角平分线定义得出∠DAE+∠ADE+∠FBC+∠BCF=180°,又根据三角形内角和定理有∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,那么∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,于是∠E+∠F=360°-(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)由(2)可知∠E+∠F=180°,如果∠E=∠F,那么可以求出∠E=∠F=90°,根据三角形内角和定理求出∠DAE+∠ADE=90°,再利用角平分线定义得到∠BAD+∠CDA=180°,于是AB∥CD.
试题解析:(1)∵∠F=70,
∴FBC+∠BCF=180°∠F=110°.
∵∠ABC、∠BCD的角平分线交于点F,
∴∠ABC=2∠FBC,∠BCD=2∠BCF,
∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=220°;
∵四边形ABCD的内角和为360°,
∴∠BAD+∠CDA=360°(∠ABC+∠BCD)=140°.
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,
∴∠DAE=![]() ∠BAD,∠ADE=
∠BAD,∠ADE=![]() ∠CDA,
∠CDA,
∴∠DAE+∠ADE=![]() ∠BAD+
∠BAD+![]() ∠CDA=
∠CDA=![]() (∠BAD+∠CDA)=70°,
(∠BAD+∠CDA)=70°,
∴∠E=180°(∠DAE+∠ADE)=110°;
故答案为:220;110;
(2)∠E+∠F=180°.理由如下:
∵∠BAD+∠CDA+∠ABC+∠BCD=360°,
∵四边形ABCD的内角∠BAD、span>∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F,
∴∠DAE+∠ADE+∠FBC+∠BCF=180°,
∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,
∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,
∴∠E+∠F=360°-(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)AB∥CD.

【题目】广州市运动员在最近八届亚运会上获得金牌的运动项目种类及金牌数量如下表所示:
田径 | 羽毛球 | 篮球 | 水球 | 网球 | 台球 | 足球 | 体操 | 游泳 | 举重 | 射击 | 击剑 | 拳击 | 赛艇 | 跳水 |
7 | 8 | 2 | 4 | 2 | 1 | 1 | 3 | 2 | 4 | 4 | 12 | 1 | 5 | 1 |
给出下列说法:①广州市运动员在最近八届亚运会上获得金牌的运动项目共有15个;②广州市运动员在最近八届亚运会上获得金牌的总数是57;③上表中,击剑类的频率约为0.211.其中正确的有( )
A. 3个
B. 2个
C. 1个
D. 0个