题目内容
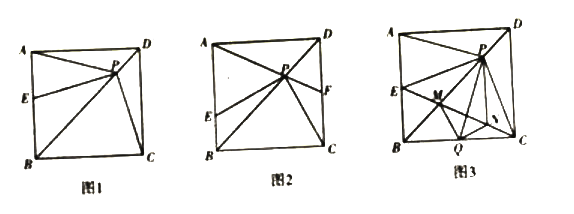
【题目】如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC,过点P作PE⊥PC交直线AB于点E.
(1)求证: PC=PE;
(2)延长AP交直线CD于点F.
①如图2,若点F是CD的中点,求△APE的面积;
②若△APE的面积是![]() ,则DF的长为_________;
,则DF的长为_________;
(3)如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ, MQ,过点P作![]() 交EC于点N,连接
交EC于点N,连接![]() ,若
,若![]() ,则
,则![]() 的面积是________.
的面积是________.
【答案】(1)略;(2)①8,②4或9;(3)![]()
【解析】
(1)利用正方形每个角都是90°,对角线平分对角的性质,三角形外角等于和它不相邻的两个内角的和,等角对等边等性质容易得证;
(2)作出△ADP和△DFP的高,由面积法容易求出这个高的值.从而得到△PAE的底和高,并求出面积.第2小问思路一样,通过面积法列出方程求解即可;
(3)根据已经条件证出△MNQ是直角三角形,计算直角边乘积的一半可得其面积.
(1) 证明:∵点P在对角线BD上,
∴△ADP≌△CDP,
∴AP=CP, ∠DAP =∠DCP,
∵PE⊥PC,∴∠EPC=∠EPB+∠BPC=90°,
∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,
∵∠PAE=90°-∠DAP=90°-∠DCP,
∠DCP=∠BPC-∠PDC=∠BPC-45°,
∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,
∴∠PEA=∠PAE,
∴PC=PE;
(2)①如图2,过点P分别作PH⊥AD,PG⊥CD,垂足分别为H、G.延长GP交AB于点M.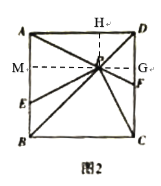
∵四边形ABCD是正方形,P在对角线上,
∴四边形HPGD是正方形,
∴PH=PG,PM⊥AB,
设PH=PG=a,
∵F是CD中点,AD=6,则FD=3,![]() =9,
=9,
∵![]() =
=![]() =
=![]() ,
,
∴![]() ,解得a=2,
,解得a=2,
∴AM=HP=2,MP=MG-PG=6-2=4,
又∵PA=PE,
∴AM=EM,AE=4,
∵![]() =
=![]() ,
,
②设HP=b,由①可得AE=2b,MP=6-b,
∴![]() =
=![]() ,
,
解得b=2.4![]() ,
,
∵![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
∴当b=2.4时,DF=4;当b=3.6时,DF=9,
即
(3)如图,
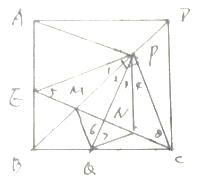
∵E、Q关于BP对称,PN∥CD,
∴∠1=∠2,∠2+∠3=∠BDC=45°,
∴∠1+∠4=45°,
∴∠3=∠4,
易证△PEM≌△PQM, △PNQ≌△PNC,
∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC,
∴∠6+∠7=90°,
∴△MNQ是直角三角形,
设EM=a,NC=b列方程组
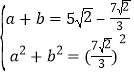 ,
,
可得![]() ab=
ab=![]() ,
,
∴![]() ,
,