题目内容
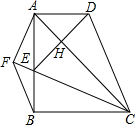 在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,延长CE于F,连接BF使BF∥CD,连接DE交对角线AC于H.
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,延长CE于F,连接BF使BF∥CD,连接DE交对角线AC于H.(1)求证:△ACD≌△ACE;
(2)若CE平分∠ACB,CE=5,求BF的长.
考点:相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,直角梯形
专题:
分析:(1)求出∠DAC=∠EAC=45°,根据SAS推出两三角形全等即可;
(2)延长DA,交BF延长线于M,延长BA、CD交于O,求出FBCA四点共圆,求出AM=AF,AF=BF,推出BM=CD=CE,即可得出BF=
CE,求出即可.
(2)延长DA,交BF延长线于M,延长BA、CD交于O,求出FBCA四点共圆,求出AM=AF,AF=BF,推出BM=CD=CE,即可得出BF=
| 1 |
| 2 |
解答:(1)证明:∵AD∥BC,∠ABC=90°,
∴∠BAD=90°,
∵AB=CB,
∴∠BAC=45°,
∴∠DAC=45°,
在△AEC和△ADC中
∴△AEC≌△ADC;
(2)解:延长DA,交BF延长线于M,延长BA、CD交于O,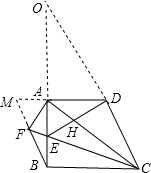
∵∠ABC=90°,AB=BC,
∴∠BAC=∠ACB=45°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=22.5°,
∵△AEC≌△ADC,
∴∠DCA=∠ACE=22.5°,
∴∠O=180°-90°-45°-22.5°=22.5°,
∵BF∥CD,
∴∠FBE=22.5°,
∴在△BCF中,∠BFC=180°-22.5°-90°-22.5°=45°=∠BAC,
∴F、A、B、C共圆,
∴∠MFA=∠BCA=45°,
∵AD∥BC,BF∥CD,
∴四边形BMDC是平行四边形,
∴BM=CD=CE,∠M=∠DCB=45°+22.5°=67.5°,
∴∠MAF=180°-67.5°-45°=67.5°=∠M,
∴AF=MF,
∵∠BAM=90°,∠FAM=67.5°,
∴∠FAB=22.5°=∠FBA,
∴AF=BF,
即BF=MF=
BM=
CE=
×5=2.5.
∴∠BAD=90°,
∵AB=CB,
∴∠BAC=45°,
∴∠DAC=45°,
在△AEC和△ADC中
|
∴△AEC≌△ADC;
(2)解:延长DA,交BF延长线于M,延长BA、CD交于O,

∵∠ABC=90°,AB=BC,
∴∠BAC=∠ACB=45°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=22.5°,
∵△AEC≌△ADC,
∴∠DCA=∠ACE=22.5°,
∴∠O=180°-90°-45°-22.5°=22.5°,
∵BF∥CD,
∴∠FBE=22.5°,
∴在△BCF中,∠BFC=180°-22.5°-90°-22.5°=45°=∠BAC,
∴F、A、B、C共圆,
∴∠MFA=∠BCA=45°,
∵AD∥BC,BF∥CD,
∴四边形BMDC是平行四边形,
∴BM=CD=CE,∠M=∠DCB=45°+22.5°=67.5°,
∴∠MAF=180°-67.5°-45°=67.5°=∠M,
∴AF=MF,
∵∠BAM=90°,∠FAM=67.5°,
∴∠FAB=22.5°=∠FBA,
∴AF=BF,
即BF=MF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形全等的判断和性质;垂直平分线的判定;直角三角形斜边上的中线等于斜边的一半;等腰直角三角形两底角都是45°,题目难度不小,有一定的综合性.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
下列说法正确的是( )
| A、-0.064的立方根是0.4 |
| B、4的平方根是±2 |
| C、-9的平方根是±3 |
| D、0.01的立方根是0.000001 |
在面积为12
的平行四边形ABCD中,AB=CD=4,AD=BC=6,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,则CE+CF的值为( )
| 2 |
A、10+5
| ||||
B、10-5
| ||||
C、10+5
| ||||
D、10+5
|
 如图,把一张矩形纸片沿对角线BD向上折叠,
如图,把一张矩形纸片沿对角线BD向上折叠,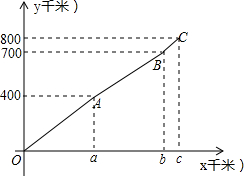 从甲地到乙地的路程为800千米,开始是平路,接着是上坡,最后是下坡.一车在甲乙两地之间往返,其在上坡、平路、下坡上的速度比都是3:4:5.该车到甲站的路程为y千米,行驶时间为x小时,y与x的函数图象如图所示.
从甲地到乙地的路程为800千米,开始是平路,接着是上坡,最后是下坡.一车在甲乙两地之间往返,其在上坡、平路、下坡上的速度比都是3:4:5.该车到甲站的路程为y千米,行驶时间为x小时,y与x的函数图象如图所示.