题目内容
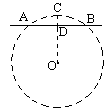
如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连结AC,DB.设CP=x,PD=y.

(1)求证:△ACP∽△DBP;
(2)求y关于x的函数解析式;
(3)若CD=8时,求S△ACP:S△DBP的值.

(1)求证:△ACP∽△DBP;
(2)求y关于x的函数解析式;
(3)若CD=8时,求S△ACP:S△DBP的值.
(1)△ACP和△DBP中,根据圆周角定理即可得到两组对应角相等,由此得证;(2)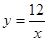 ;(3)4:9或4:1.
;(3)4:9或4:1.
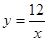 ;(3)4:9或4:1.
;(3)4:9或4:1.试题分析:(1)△ACP和△DBP中,根据圆周角定理即可得到两组对应角相等,由此得证;
(2)根据相似三角形得到的比例线段即可求出y、x的函数关系式;
(3)已知CD=CP+PD=8,联立(2)的函数关系式,即可求得CP、PD的长,进而可根据相似三角形的面积比等于相似比的平方得出所求的结果.
(1)∵∠A=∠D,∠C=∠B,∴△ACP∽△DBP;
(2)由(1)得CP:BP=AP:PD即
 ,解得
,解得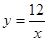 ;
;(3)由CD=8即
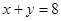 和
和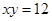 解得
解得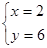 或
或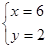
则S△ACP:S△DBP=4:9或4:1.
点评:解题的关键是熟练掌握圆周角定理:同弧等等弧所对的圆周角相等,都等于所对圆心角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
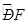 的中点.
的中点. 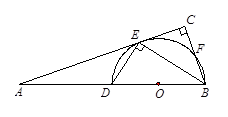
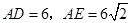 ,求
,求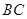 的长.
的长.
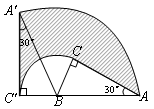

 ,则弦CD的长为( )
,则弦CD的长为( )




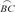 的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm,CE=2cm,下列结论错误的是( )
的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm,CE=2cm,下列结论错误的是( )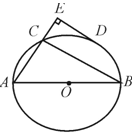
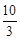 cm时,量得锯痕AB=
cm时,量得锯痕AB=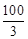 cm,问圆木的直径是多少cm?
cm,问圆木的直径是多少cm?