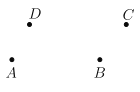题目内容
【题目】已知,等腰直角△ABC在平面直角坐标系中的位置如图,点A(0,a),点B(b,0)，点C在第四象限，且满足a2+b2-4a+12b+40=0.
(1)求点C的坐标；
(2)若AC交x轴于M，BC交y轴于D，E是AC上一点，且CE=AM，连DM，求证：AD+DE=BM；
(3)在y轴上取点F(0,6),点H是y轴上F下方任一点,作HG⊥BH交射线CF于G,在点H位置变化的过程中,
是否为定值，若是，求其值，若不是，说明理由.
【答案】（1）C（2，-4） （2）见解析 （3）是定值，值为1
【解析】
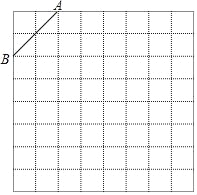
（1）根据题意可求得A、B两点坐标，作CT⊥y轴于T．只要证明△ABO≌△CAT，可得CT=OA=2，AT=OB=6，由此即可解决问题；
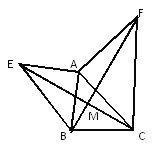
（2）如图2中，作CK⊥AC交y轴于K．只要证明△ABM≌△CAK，△CDE≌△CDK即可解决问题；
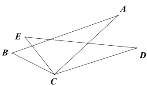
（3）结论：
=1．作AI⊥AF交FB的延长线于I，作HJ⊥BF于J，HK⊥GF于K．想办法证明△HJB≌△HKG，可得BH=GH即可解决问题；
（1）∵a2+b2-4a+12b+40=0.
∴
∴a=2，b=-6
故A(0,2)，B(-6,0)
如图1中，作CT⊥y轴于T．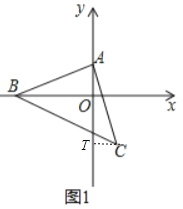
∵∠AOB=∠BAC=∠ATC=90°，
∴∠ABO+∠BAO=90°，∠BAO+∠CAT=90°，
∴∠ABO=∠CAT，
∵AB=AC，
∴△ABO≌△CAT，
∴CT=OA=2，AT=OB=6，
∴OT=AT=AO=4，
∴C（2，-4）．
（2）如图2中，作CK⊥AC交y轴于K．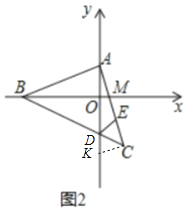
∵∠BAM=∠ACK=90°，AB=AC，∠ABM=∠CAK，
∴△ABM≌△CAK，
∴AM=CK，BM=AK，
∵CE=AM，
∴CE=CK，
∵DC=DC，∠DCE=∠DCK，
∴△CDE≌△CDK，
∴DE=DK，
∴AD+DE=AD+DK=AK=BM．
（3）是定值.结论： =1．
理由：作AI⊥AF交FB的延长线于I，作HJ⊥BF交BF的延长线于J，HK⊥GF于K．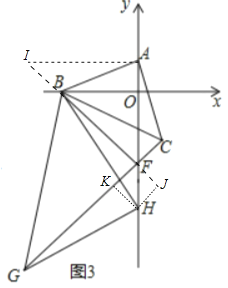
∵B（-6，0），F（0，-6），
∴OB=OF，
∴△BOF是等腰直角三角形，
∴∠AFB=45°，
∵AI⊥AF，
∴∠I=∠AFI=45°，
∴AI=AF，
∵∠BAC=∠IAF=90°，
∴∠IAB=∠FAC，
∵AI=AF，AB=AC，
∴△AIB≌△AFC，
∴∠CFA=∠I=45°
∴∠BFC=90°，
∵∠BFC=∠CFO=45°，∴∠GFH=∠HFJ=45°，
∴HK=HJ，
∵∠BFG=∠BHG，
∴∠HBF=∠HGF，
∴△HJB≌△HKG，
∴BH=GH，
∴=1．
