题目内容
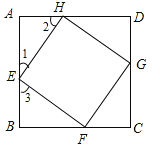
【题目】如图，正方形EFGH的顶点在边长为2的正方形的边上．若设AE=x，正方形EFGH的面积为y，则y与x的函数关系为 ．
【答案】
（0＜x＜2）．
【解析】
试题分析：如图所示，∵四边形ABCD是边长为1的正方形，∴∠A=∠B=90°，AB=2，∴∠1+∠2=90°，∵四边形EFGH为正方形，∴∠HEF=90°，EH=EF，∴∠1+∠3=90°，∴∠2=∠3，在△AHE与△BEF中，∵∠A=∠B，∠2=∠3，EH=FE，∴△AHE≌△BEF（AAS），∴AE=BF=x，AH=BE=2﹣x，在Rt△AHE中，由勾股定理得：EH2=AE2+AH2=x2+（2﹣x）2=2x2﹣4x+4；即（0＜x＜2），故答案为：（0＜x＜2）．
练习册系列答案
步步高达标卷系列答案
相关题目
