Question

【题目】如图，△ABC中，∠C=90°，AC=4，BC=3．半径为1的圆的圆心P以1个单位/S的速度由点A沿AC方向在AC上移动，设移动时间为t（单位：s）．

（1）当t为何值时，⊙P与AB相切；
（2）作PD⊥AC交AB于点D，如果⊙P和线段BC交于点E．求当t为何值时，四边形PDBE为平行四边形．

Answer 1

【答案】
（1）解：∵过P作PH⊥AB于H，

又∵⊙P与AB相切，

∴PH=1，

∴∠AHP=∠C=90°，∠A=∠A，

∴△APH∽△ABC，

∴ ，

∵△ABC中，∠C=90°，AC=4，BC=3，

∴AB= =5，

∴ ，

∴AP= ，

∴当t= 时，⊙P与AB相切

（2）解：∵PD⊥AC，∠C=90°，

∴PD∥BE，

∴当PE∥AB时，四边形PDBE为平行四边形．

∴△CPE∽△CAB，

∴ ，

∴ ，

∴CP= ，

∴AP=AC﹣CP= ，

∴当t= 时，四边形PDBE为平行四边形．

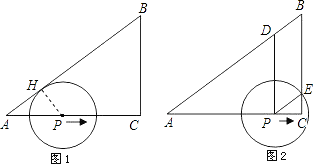
【解析】（1）首先过P作PH⊥AB于H，由⊙P与AB相切，可得PH=1，易证得△APH∽△ABC，根据相似三角形的对应边成比例，可得 ，继而求得AP的长；即可得当t为何值时，⊙P与AB相切；（2）由PD⊥AC，∠C=90°，可证得PD∥BC，继而可得当PE∥AB时，四边形PDBE为平行四边形，则可得△CPE∽△CAB，然后由相似三角形的对应边成比例，求得CP的长，继而求得答案．