��Ŀ����
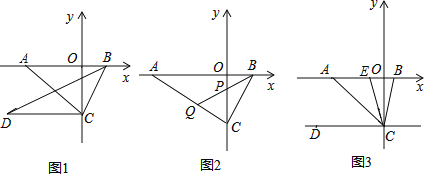
����Ŀ��һ�п쳵�ɼؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ�����������˶����쳵���ҵص�·��y1��km������ʻ��ʱ��x��h��֮��ĺ�����ϵ����ͼ���߶�AB��ʾ���������ҵص�·��y2��km������ʻ��ʱ��x��h�� ֮��ĺ�����ϵ����ͼ���߶�OC��ʾ������ͼ���������̽������1���ס�������֮��ľ���Ϊ�� ��km����2���߶�AB�Ľ���ʽΪ�� �����߶�OC�Ľ���ʽΪ�� ������3����졢����֮��ľ���Ϊy��km������ֱ��д��y����ʻʱ��x��h���ĺ�����ϵʽ��

���𰸡���1��450km����2��![]() =��150x+450��0��x��3����OC�Ľ���ʽ��
=��150x+450��0��x��3����OC�Ľ���ʽ�� ![]() =75x��0��x��6��
=75x��0��x��6��
��3��y=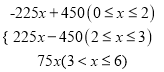 ��
��
�������������������1������A������Ϊ��0��450�������Եó��ף�������֮��ľ��룻��2������A������Ϊ��0��450����B������Ϊ��3��0��������y1=kx+b������ɣ������߶�OC����ʽΪy2=mx ���m���ɣ���3����y1=y2����150x+450=75x�����x=2���֢ٵ�0��x��2ʱ��y=y1��y2������2��x��3ʱ��y=y2��y1������3��x��6ʱ��y=y2�����������������ʽ����.
���ã�2��������ó���y=|y1-y2|���������������ʽ���ó�ͼ�ɣ�
���������
��1���ߵ�x=0ʱ��y1=450��
��ס�������֮��ľ���Ϊ450km��
�ʴ�Ϊ��450��
��2�����߶�AB�Ľ���ʽΪy1=kx+b���߶�OC�Ľ���ʽΪy2=mx��
����A��0��450����B��3��0������y1=kx+b��
![]() ����ã�
����ã�![]() ��
��
���߶�AB�Ľ���ʽΪy1=��150x+450��0��x��3����
����C��6��450������y2=mx��
6m=450����ã�m=75��
���߶�OC�Ľ���ʽΪy2=75x��0��x��6����
�ʴ�Ϊ��y1=��150x+450��0��x��3����y2=75x��0��x��6����
��3����y1=y2����150x+450=75x��
��ã�x=2��
��0��x��2ʱ��y=y1��y2=��150x+450��75x=��225x+450��
��2��x��3ʱ��y=y2��y1=75x������150x+450��=225x��450��
��3��x��6ʱ��y=y2=75x��
��졢����֮��ľ���y��km������ʻʱ��x��h���ĺ�����ϵʽΪy=![]() ��
��

����Ŀ��ij��ժũ���ƻ���ֲA��B���ֲ�ݮ��6Ķ�����ݱ�����Ϣ������������⣺
��Ŀ Ʒ�� | A | B |
��Ķ������λ��ǧ�ˣ� | 1200 | 2000 |
��ժ�۸� | 60 | 40 |
��1������ũ��ÿ���ݮȫ������ժ��������Ϊ460000Ԫ����ôA��B���ֲ�ݮ���ֶ���Ķ��
��2����Ҫ����ֲA�ֲ�ݮ��Ķ����������ֲB�ֲ�ݮ��һ�룬��ô��ֲA�ֲ�ݮ����Ķʱ����ʹ��ũ��ÿ���ݮȫ������ժ����������ࣿ�������������룮