题目内容
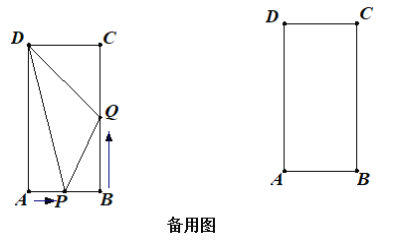
【题目】如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发沿AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿BC以2cm/s的速度向点C移动．设运动时间为t秒.
（1）当t＝2时，△DPQ的面积为 cm2；
（2）在运动过程中△DPQ的面积能否为26cm2？如果能，求出t的值，若不能，请说明理由；
（3）运动过程中，当 A、P、Q、D四点恰好在同一个圆上时，求t的值；
（4）运动过程中，当以Q为圆心，QP为半径的圆，与矩形ABCD的边共有4个交点时，直接写出t的取值范围．
【答案】（1）28；（2）△DPQ的面积不可能为26cm2；（3）t＝6或
时A、P、Q、D四点恰好在同一个圆上；（4）当
＜t＜
时，⊙Q与矩形ABCD的边共有四个交点．
【解析】
（1）根据运动速度表示出长度，然后计算出三个直角三角形面积，再由矩形面积减去三个直角三角形面积就能得到△DPQ的面积；
（2）根据（1）总得出的面积计算方式，列出关于t的方程，通过判断方程有无解来即可判断；
（3）△DAP是直角三角形如果它的三个顶点都在圆上，可得DP是直径，Q也要在圆上，那么△DQP也是直角三角形，通过勾股定理用t表示出DP、PQ、DQ，再由DP=PQ+DQ列出方程求解即可；
（4）判断出⊙Q与边AD相切和⊙Q过D点是从有4个交点变成3个交点的时刻，再根据半径相等列出关于t的方程求解.
由题意得AP=
，BQ=
∴PB=AB-AP=6-2=4，CQ=CB-BQ=12-4=8
∴
=
，
=
，
=
∴
=
---=72-12-8-24=28（cm2）
（2）法一：根据题意得
=
整理得
∵ b2－4ac＝－4＜0，
∴方程无实数根
∴△DPQ的面积不可能为26cm2
法二：
=
当t＝3时，△DPQ的面积有最小值为27 cm2
∴△DPQ的面积不可能为/span>26cm2
（3）∵∠A＝90°
∴A、P、D三点在以DP为直径的圆上
若点Q也在圆上，则∠PQD＝90°
∵PQ2＝(6－t)2＋(2t)2，DQ2＝62＋(12－2t)2，DP2＝t2＋122
当PQ2＋DQ2＝ DP2，∠PQD＝90°
∴(6－t)2＋(2t)2＋62＋(12－2t)2＝ t2＋122
解得t1＝6,t2＝
∴t＝6或时A、P、Q、D四点恰好在同一个圆上．
（4）如右图1，
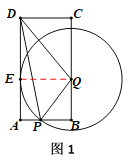
⊙Q与边AD相切
过点Q作QE⊥AD
∵⊙Q与边AD相切
∴QE＝QP
62＝(6－t)2＋(2t)2
解得t1＝0（舍去）,t2＝
如右图2，
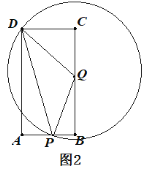
⊙Q与过点D
则QD＝QP
(6－t)2＋(2t)2＝62＋(12－2t)2
（舍去）
∴当＜t＜时，⊙Q与矩形ABCD的
边共有四个交点．
