题目内容
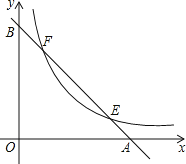
【题目】已知二次函数y=x2﹣（m﹣1）x﹣m，其中m＞0，它的图象与x轴从左到右交于R和Q两点，与y轴交于点P，点O是坐标原点．下列判断中不正确的是（ ）
A.方程x2﹣（m﹣1）x﹣m=0一定有两个不相等的实数根B.点R的坐标一定是（﹣1，0）
C.△POQ是等腰直角三角形D.该二次函数图象的对称轴在直线x=﹣1的左側
【答案】D
【解析】
先依据因式分解法求得方程的两根，然后再将x=0代入求得点P的纵坐标，从而可求得问题的答案．
解：令y=0得x2﹣（m﹣1）x﹣m=0，则（x+1）（x﹣m）=0，
解得：x1=﹣1，x2=m．
∵m＞0＞﹣1，
∴R（﹣1，0）、Q（m，0）．
∴方程由两个不相等的实数根．
∴A、B正确，与要求不符；
当x=0，y=﹣m，
∴P（0，﹣m）．
∴OP=OQ．
∴△OPQ为等腰直角三角形．
∴C正确，与要求不符；
∵抛物线的对称轴为x=﹣
，m＞0，
∴x＞﹣
．
∴D错误，与要求相符．
故选：D．
【题目】某工厂为了检验甲、乙两个车间生产的同一款产品的质量情况，进行了抽样调查，请补充完整．
收集数据 从甲、乙两个车间各随机抽取20个样品，进行了检测，检测结果（单位：mm）如下：
甲车间 | 168 | 175 | 180 | 185 | 172 | 189 | 185 | 182 | 185 | 174 |
192 | 180 | 185 | 178 | 173 | 185 | 169 | 187 | 176 | 180 | |
乙车间 | 186 | 180 | 189 | 183 | 176 | 173 | 178 | 167 | 180 | 175 |
178 | 182 | 180 | 179 | 185 | 180 | 184 | 182 | 180 | 183 |
整理、描述数据 按如下分段整理、描述这两组样本数据：
165.5-170.5 | 170.5-175.5 | 175.5-180.5 | 180.5-185.5 | 185.5-190.5 | 190.5-195.5 | |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 |
（说明：尺寸范围为176mm～190mm的产品为合格）
分析数据 两组样本数据的平均数、众数、中位数、方差如下表所示：
平均数 | 众数 | 中位数 | 方差 | |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
得出结论
（1）补全上列表格；
（2）若乙车间生产1000个该款产品，估计其中合格产品约有 个；
（3）可以推断出 车间生产的该款产品更好，理由为
【题目】甲、乙两店销售同一种蔬菜种子．在甲店，不论一次购买数量是多少，价格均为4.5元
．在乙店价格为5元，如果一次购买2kg以上的种子，超出2kg部分的种子价格打8折．设小明在同一个店一次购买种子的数量为
（
）．
（1）根据题意填表：
一次购买数量∕ | 1.5 | 2 | 3.5 | 6 | … |
在甲店花费∕元 | 6.75 | 15.75 | … | ||
在乙店花费∕元 | 7.5 | 16 | … |
（2）设在甲店花费
元，在乙店花费
元，分别求，关于
的函数解析式；
（3）根据题意填空：
① 若小明在甲店和在乙店一次购买种子的数量相同，且花费相同，则他在同一个店一次购买种子的数量为 
；
② 若小明在同一个店一次购买种子的数量为3kg，则他在甲、乙两个店中的 店购买花费；
③ 若小明在同一个店一次购买种子花费了45元，则他在甲、乙两个店中的 店购买数量多．
