题目内容
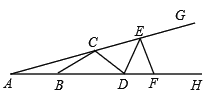
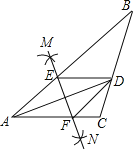
【题目】如图,在![]() 中,AD平分
中,AD平分![]() ,按如下步骤作图:
,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD两侧作弧,交于两点M、N;
的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若![]() ,
,![]() ,
,![]() ,求BD的长是______.
,求BD的长是______.
【答案】![]()
【解析】
利用基本作图得MN垂直平分AD,则AE=DE,FA=FC,再证明四边形AEDF为菱形得到AE=AF=4,DE∥AC,然后利用平行线分线段成比例定理计算BD的长.
解:由作法得MN垂直平分AD,则AE=DE,FA=FC,
∵AD平分∠EAF,AD⊥EF,
∴△AEF为等腰三角形,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF为菱形,
∴AE=AF=4,DE∥AC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BD=![]()
故答案为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目