题目内容
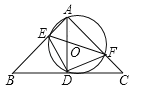
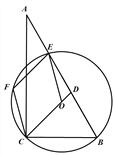
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,经过B,C两点的⊙O交边AB于另一点E,延长CO交边AB于点D,EF∥CD交⊙O于另一点F, 连接CF。
(1)若⊙O的半径为4,求弧CE的长;
(2)求证:四边形EFCO是菱形;
(3)若BC=6,tan∠CDB=3,求BD的长。
【答案】(1)![]() (2)证明见解析(3)3+
(2)证明见解析(3)3+![]()
【解析】分析:(1)根据圆周角定理可得∠COE=120°,再根据弧长计算公式即可得解;
(2)如图,连接OF,易证△OEF和△OCF是等边三角形,得EF=OE=CF=OC,故得四边形EFCO是菱形;
(3)作CH⊥AB于点H,可得∠CHD=∠CHE=90°,在Rt△CHB中,∠ABC=60°,BC=6,故BH=3,CH=![]() .在Rt△CHD中,tan∠CDB=3,故DH=
.在Rt△CHD中,tan∠CDB=3,故DH=![]() CH=
CH=![]() ,故BD=3+
,故BD=3+![]() .
.
(1)∵∠ACB=90°,∠A=30°,
∴∠ABC=60°
∴∠COE=120°
∴弧CE的长![]()
(2)如图,连接OF,
∵∠COE=120°,
∴∠DOE=60°,
∵EF∥CD,
∴∠OEF=60°,
∵OE=OF,
∴△OEF是等边三角形,
∴EF= OE =r,∠FOE=60°,
∴∠COE=∠COE-60°=60°,
∵OC=OF,
∴△OCF是等边三角形,
∴CF=OC=r,
∴EF=OE=CF=OC,
∴四边形EFCO是菱形.
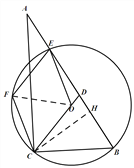
(3)作CH⊥AB于点H,可得∠CHD=∠CHE=90°,
在Rt△CHB中,
∵∠ABC=60°,BC=6,
∴BH=3,CH=![]() .
.
在Rt△CHD中,tan∠CDB=3,
∴DH=![]() CH=
CH=![]() ,
,
∴BD=3+![]() .
.

练习册系列答案
相关题目