题目内容
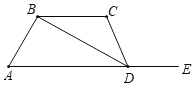
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练,机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动,已知AD=6个单位长度,机器人的速度为1个单位长度/s且其移动至拐角处调整方向所需时间忽略不计.设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)图②中函数图象与纵轴的交点的纵坐标![]() 在图①中表示一条线段的长,请在图①中画出这条线段.
在图①中表示一条线段的长,请在图①中画出这条线段.
(2)求图②中a的值;
(3)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.

【答案】(1)详见解析;(2)a=8;(3)t1=11,t2=18.
【解析】试题分析:(1)作![]() 垂足为T,由题意得到
垂足为T,由题意得到![]()
![]() 即为所求.
即为所求.
![]() 在
在![]() 中,根据勾股定理得到
中,根据勾股定理得到![]() 根据
根据![]() ,得到
,得到![]() 求出
求出![]() ,即可得到结论;
,即可得到结论;
![]() 如图,在图①中连接
如图,在图①中连接![]() ,分别过
,分别过![]() 作BD的垂线,垂足分别为
作BD的垂线,垂足分别为![]() 则
则![]() ∥
∥![]() ,根据平行线的性质得到
,根据平行线的性质得到![]() ,得到
,得到![]() .根据平行线分线段成比例定理得到
.根据平行线分线段成比例定理得到![]() 求得
求得![]() 于是得到结论.
于是得到结论.
试题解析:(1)作![]() 垂足为T,则
垂足为T,则![]()
![]() 即为所求.
即为所求.
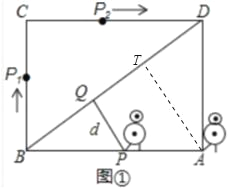
(2)在![]() 中,
中, ![]()
![]()
![]()
由题意得: ![]()
![]()
∴![]()
∴![]() ,即
,即![]()
(3)在图①中连接![]() ,分别过
,分别过![]() 作BD的垂线,垂足分别为
作BD的垂线,垂足分别为![]() 则
则![]() ∥
∥![]() ,
,
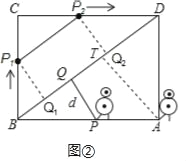
∵在图②中,线段MN平行于横轴,
![]() 即
即![]() 又
又![]() ∥
∥![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ∥
∥![]() ,
,
∴![]() 即有
即有![]()
![]()
![]()
由题意得: ![]()
![]()

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目