题目内容
【题目】如图，直线y=kx+2k（k≠0）与x轴交于点B，与双曲线
交于点A、C，其中点A在第一象限，点C在第三象限．
（1）求B点的坐标；
（2）若S△AOB=2，求A点的坐标；
（3）在（2）的条件下，在y轴上是否存在点P，使△AOP是等腰三角形？若存在，请直接写出P点的坐标．
【答案】（1）（﹣2，0）；（2）（2，2）；（3）（0，2），（0，4），（0， 
），（0， 
）
【解析】（1）利用y=kx+2k，当y=0时，可以求出x的值，从而求出B的坐标；
（2）设点A坐标为（a，b），OB=2，根据S△AOB=2可以求出b，然后求出a，也就求出了A的坐标；
（3）利用△AOP是等腰三角形，而腰与底没有确定，所以分类讨论即可．
解：（1）对于y=kx+2k，当y=0时，x=﹣2，
∴B点坐标为（﹣2，0）；
（2）设点A坐标为（a，b），
∵点A在第一象限，
∴a＞0，b＞0，
∵S△AOB=2，
∴
，
∴b=2，
∵点A在双曲线上，
∴a=2，
∴A坐标为（2，2）；
（3）符合条件的点P有4个，坐标为：
（0，2），（0，4），（0， 
），（0， 
）．
练习册系列答案
相关题目
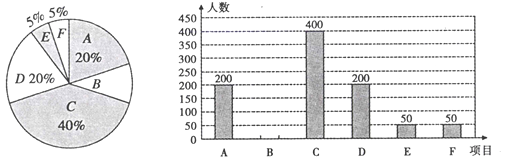
【题目】某校举行“汉字听写”比赛，每名学生听写汉字39个，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
根据以上信息解决下列问题：
(1)在统计表中，
______，
______；
(2)请补全频数分布直方图.
(3)扇形统计图中“C”对应扇形的圆心角的度数是_______.
(4)若该校共有1200名学生参加此次“汉字听写”比赛，估计此次参加比赛听写正确字数不低于24个的学生人数.
