Question

如图，以点P为圆心的圆弧与X轴交于A，B两点，点P的坐标为（4，2）点A的坐标（2，0）则点B的坐标为         ．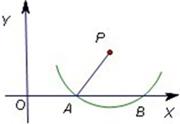

Answer 1

(6,0)

试题分析:连接PA、PB．过点P作PD⊥AB于点D．根据两点间的距离公式求得PA=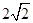；然后由已知条件“点P为圆心的圆弧与x轴交于A、B两点”知PA=PB=2；再由垂径定理和勾股定理求得AD=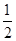
AB=2，所以AB=4，由两点间的距离公式知点B的坐标．连接PA、PB．过点P作PD⊥AB于点D．∵P（4，2）、A（2，0），∴PA=PB=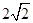，PD=2；∵点P为圆心的圆弧与x轴交于A、B两点，，AB是垂直于直径的弦，∴AD=DB；在直角三角形PDA中，AD²=AP²-PD²，∴AD=2；∴AB=4，∴B（6，0）．
点评：此类试题属于难度很大的试题，此类试题的解答只要把握好垂径定理的定义和公式的解法