题目内容
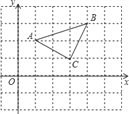
【题目】如图1，在平面直角坐标系，O为坐标原点，点A（﹣1，0），点B（0， 
）．
（1）求∠BAO的度数；
（2）如图1，将△AOB绕点O顺时针得△A′OB′，当A′恰好落在AB边上时，设△AB′O的面积为S1 ， △BA′O的面积为S2 ， S1与S2有何关系？为什么？
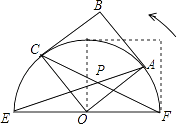
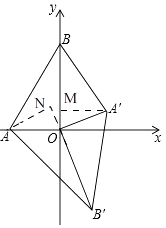
（3）若将△AOB绕点O顺时针旋转到如图2所示的位置，S1与S2的关系发生变化了吗？证明你的判断．
【答案】
（1）
解：∵A（﹣1，0），B（0， 
），
∴OA=1，OB= ，
在Rt△AOB中，tan∠BAO= 
= ，
∴∠BAO=60°
（2）
解：∵∠BAO=60°，∠AOB=90°，
∴∠ABO=30°，
∴CA'=AC= 
AB，
∴OA'=AA'=AO，
根据等边三角形的性质可得，△AOA'的边AO、AA'上的高相等，
∴△BA'O的面积和△AB'O的面积相等（等底等高的三角形的面积相等），
即S1=S2
（3）
解：S1=S2不发生变化；
理由：如图，过点'作A'M⊥OB．过点A作AN⊥OB'交B'O的延长线于N，
∵△A'B'O是由△ABO绕点O旋转得到，
∴BO=OB'，AO=OA'，
∵∠AON+∠BON=90°，∠A'OM+∠BON=180°﹣90°=90°，
∴∠AON=∠A'OM，
在△AON和△A'OM中，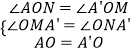 
，
∴△AON≌△A'OM（AAS），
∴AN=A'M，
∴△BOA'的面积和△AB'O的面积相等（等底等高的三角形的面积相等），
即S1=S2．
【解析】（1）先求出OA，OB，再用锐角三角函数即可得出结论；（2）根据等边三角形的性质可得AO=AA'，再根据直角三角形30°角所对的直角边等于斜边的一半求出AO= AB，然后求出AO=OA'，再根据等边三角形的性质求出点O到AB的距离等于点A'到AO的距离，然后根据等底等高的三角形的面积相等解答；（3）根据旋转的性质可得BO=OB'，AA'=OA'，再求出∠AON=∠A'OM，然后利用“角角边”证明△AON和△A'OM全等，根据全等三角形对应边相等可得AN=A'M，然后利用等底等高的三角形的面积相等证明．
【考点精析】认真审题，首先需要了解等边三角形的判定(三个角都相等的三角形是等边三角形；有一个角等于60°的等腰三角形是等边三角形)，还要掌握旋转的性质(①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了)的相关知识才是答题的关键．
