题目内容
【题目】如图,在平行四边形![]() 中,
中,![]() ,
, ![]() ,
,![]() ,
,![]() , 垂足为
, 垂足为![]() ,在平行四边形的边上有一点
,在平行四边形的边上有一点![]() ,且
,且![]() .将平行四边形折叠,使点
.将平行四边形折叠,使点![]() 与点
与点![]() 合,折痕所在直线与平行四边形交于点
合,折痕所在直线与平行四边形交于点![]() 、
、![]() .
.

(1)求![]() 的长;
的长;
(2)请补全图形并求折痕![]() 的长.
的长.
【答案】(1)![]() ;(2)补全图形见解析;折痕
;(2)补全图形见解析;折痕![]() 的长为5或
的长为5或![]() .
.
【解析】
(1)在Rt△ADE中,![]() ,
,![]() ,求得
,求得![]() ,再根据勾股定理即可求解;
,再根据勾股定理即可求解;
(2)分点O在AB和AD两类讨论,当点![]() 在
在![]() 上时,可得
上时,可得![]() 是等边三角形.求得
是等边三角形.求得![]() ;点点O在AD上时,过点
;点点O在AD上时,过点![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,
,
垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,![]() .求出
.求出![]() ,
,![]() ,
,![]() ,
,![]() 根据折叠性质,结合勾股定理,求出
根据折叠性质,结合勾股定理,求出![]() ,进而求出
,进而求出![]() ,利用面积法即可求得
,利用面积法即可求得![]() .
.
(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)如图1所示,当点![]() 在
在![]() 上时,
上时,
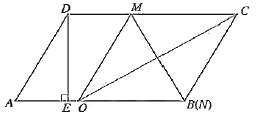
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵将平行四边形折叠,使点![]() 与点
与点![]() 重合,
重合,
∴折痕![]() 垂直平分
垂直平分![]() ,即
,即![]() ,
,
![]() .
.
∵折痕![]() 与平行四边形
与平行四边形![]() 的边
的边![]() 交于点
交于点![]() ,
,
∴点![]() 与点
与点![]() 重合.
重合.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
如图2所示,当点![]() 在
在![]() 上时,
上时,
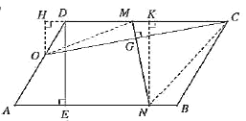
过点![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,
,
垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() ,
,
![]() .
.
∴在![]() 中,
中,![]() ,
,
由折叠可知,![]() ,
,![]() .
.
∴在![]() 中,
中,![]() ,
,
即![]() .
.
∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∴四边形![]() 为矩形.
为矩形.
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() .
.
综上所述,折痕![]() 的长为5或
的长为5或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目