题目内容
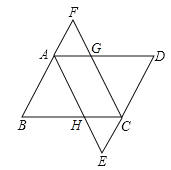
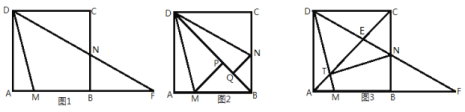
【题目】如图，在四边形ABCD中，∠A＝∠C＝90°，DE，BF分别平分∠ADC，∠ABC，并交线段AB，CD于点E，F（点E，B不重合）．在线段BF上取点M，N（点M在BN之间），使BM＝2FN．当点P从点D匀速运动到点E时，点Q恰好从点M匀速运动到点N．记QN＝x，PD＝y，已知
，当Q为BF中点时，
．
（1）判断DE与BF的位置关系，并说明理由；
（2）求DE，BF的长；
（3）若AD＝6．①当DP＝DF时，通过计算比较BE与BQ的大小关系；②连结PQ，当PQ所在直线经过四边形ABCD的一个顶点时，求所有满足条件的x的值．
【答案】（1）
，理由见解析；（2）
；（3）①
；②
【解析】
（1）推出∠AED=∠ABF，即可得出DE∥BF；
（2）求出DE=12，MN=10，把
代入
，解得：x=6，得到NQ=6，得出QM=4，由FQ=QB，BM=2FN，得出FN=2，BM=4，即可得出结果；
（3）①连接EM并延长交BC于点H，易证四边形DFME是平行四边形，得出DF=EM，求出∠DEA=∠FBE=∠FBC=30°，∠ADE=∠CDE=∠FME=60°，∠MEB=∠FBE=30°，得出∠EHB=90°，DF=EM=BM=4，MH=2，EH=6，由勾股定理得
，
,当DP=DF时 ，求出
，得到BQ＞BE；
②（Ⅰ）当PQ经过点D时，y=0，则x=10；
（Ⅱ）当PQ经过点C时，由FQ∥DP，得出△CFQ∽△CDP，则
，即可求得
；
（Ⅲ）当PQ经过点A时，由PE∥BQ，得出△APE∽△AQB，则
，根据勾股定理得
,则
，
；由图可知，PQ不可能过点B．
解：（1）DE与BF的位置关系为：DE∥BF，理由如下：
如图1所示：
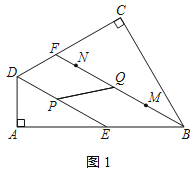
∵∠A=∠C=90°，
∴∠ADC+∠ABC=360°-（∠A+∠C）=180°，
∵DE、BF分别平分∠ADC、∠ABC，
∵∠ADE+∠AED=90°，
∴∠AED=∠ABF，
∴DE∥BF；
（2）令x=0，得y=12，
∴DE=12，
令y=0，得x=10，
∴MN=10，
把代入，
解得：x=6，即NQ=6，
∴QM=10-6=4，
∵Q是BF中点，
∴FQ=QB，
∵BM=2FN，
∴FN+6=4+2FN，
解得：FN=2，
∴BM=4，
∴BF=FN+MN+MB=16；
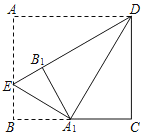
（3）①连接EM并延长交BC于点H，如图2所示：
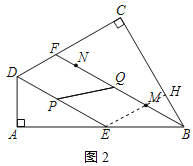
∵FM=2+10=12=DE，DE∥BF，
∴四边形DFME是平行四边形，
∴DF=EM，
∵AD=6，DE=12，∠A=90°，
∴∠DEA=30°，
∴∠DEA=∠FBE=∠FBC=30°，
∴∠ADE=60°，
∴∠ADE=∠CDE=∠FME=60°，
∴∠DFM=∠DEM=120°，
∴∠MEB=180°-120°-30°=30°，
∴∠MEB=∠FBE=30°，
∴∠EHB=180°-30°-30°-30°=90°，DF=EM=BM=4，
，
∴EH=4+2=6，
由勾股定理得：
，
∴
，
当DP=DF时，
，
解得：
，
，
，
BQ＞BE；
②（Ⅰ）当PQ经过点D时，如图3所示：
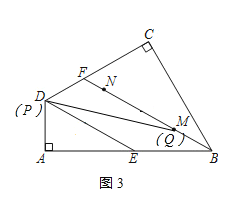
y=0，则x=10；
（Ⅱ）当PQ经过点C时，如图4所示：
∵BF=16，∠FCB=90°，∠CBF=30°，
，
CD=8+4=12，
∵FQ∥DP，
∴△CFQ∽△CDP，
∴ ，
∴
，
解得： ；
（Ⅲ）当PQ经过点A时，如图5所示：
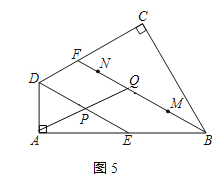
∵PE∥BQ，
∴△APE∽△AQB，
∴ ，
根据勾股定理得：
,
∴
，
，
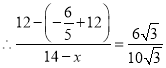解得： ；
由图可知，PQ不可能过点B；
综上所述，当x=10或或时，PQ所在的直线经过四边形ABCD的一个顶点．
