题目内容
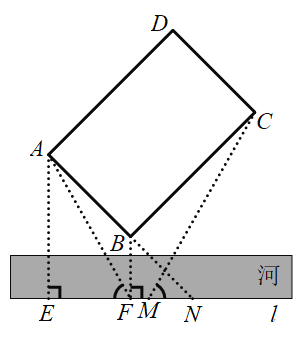
【题目】如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为_______米,BC为_______米.
【答案】![]()
![]()
【解析】
过点C作CP⊥EF于点P,过点B作直线GH∥EF交AE于点G,交CP于点H,如图,则△ABG、△BCH都是等腰直角三角形,四边形BGEF、BHPF是矩形,于是可根据等腰直角三角形的性质和勾股定理依次求出AG、BG、AB的长,设FP=BH=CH=x,则MP=x-2,CP=x+10,易证△AEF∽△CPM,然后根据相似三角形的性质即可得到关于x的方程,解方程即可求出x,再根据勾股定理即可求出BC的长.
解:过点C作CP⊥EF于点P,过点B作直线GH∥EF交AE于点G,交CP于点H,如图,则GH⊥AE,GH⊥CP,
∴四边形BGEF、BHPF是矩形,
∵∠ANE=45°,∴∠NAE=45°,
∴AE=EN=EF+FM+MN=15+2+8=25,
∵∠ABG=45°,∴∠GAB=45°,
∴AG=BG=EF=15,
∴![]() ,GE=BF=PH=10,
,GE=BF=PH=10,
∵∠ABG=45°,∠ABC=90°,∴∠CBH=45°,
∴∠BCH=45°,∴BH=CH,
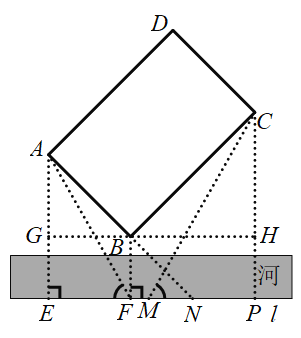
设FP=BH=CH=x,则MP=x-2,CP=x+10,
∵∠1=∠2,∠AEF=∠CPM=90°,
∴△AEF∽△CPM,
∴![]() ,即
,即![]() ,解得:x=20,
,解得:x=20,
即BH=CH=20,
∴![]() .
.
∴![]() 米,
米,![]() 米.
米.
故答案为:![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目