Question

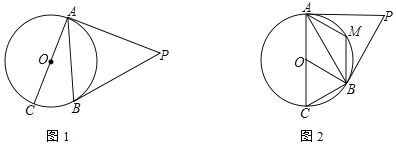
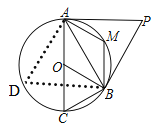
【题目】如图，AC是⊙O的直径，PA、PB是⊙O的切线，切点分别是点A、B

（1）如图1，若∠BAC=25°，求∠P的度数．

（2）如图2，若M是劣弧AB上一点，∠AMB=∠AOB，求∠P的度数．

Answer 1

【答案】（1）50°；（2）60°．

【解析】

（1）先根据切线长定理得到PA=PB，则利用等腰三角形的性质得∠PAB=∠PBA，再根据切线的性质得∠CAP=90°，于是利用互余计算出∠PAB=65°，然后根据三角形内角和定理计算∠P的度数．
（2）在弧AC上取一点D，连接AD，CD，利用已知条件和圆的内接四边形的性质即可求出∠P的度数．

（1）∵PA，PB是⊙O的切线，

∴PA=PB，

∴∠PAB=∠PBA．

∵PA为切线，

∴CA⊥PA，

∴∠CAP=90°．

∵∠BAC=25°，

∴∠PAB=90°﹣∠BAC=65°，

∴∠P=180°﹣2∠PAB=50°；

（2）在弧AC上取一点D，连接AD，BD，

∴∠AOB=2∠ADB．

∵∠AMB+∠ADB=180°，∠AMB=∠AOB，

∴∠ADB+2∠ADB=180°，

∴∠ADB=60°，

∴∠AOB=120°，

∴∠P=360°﹣90°﹣90°﹣120°=60°．