题目内容
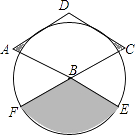
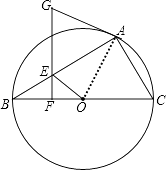
【题目】如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE. 
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
【答案】
(1)证明:如图,
连接OA,
∵OA=OB,GA=GE
∴∠ABO=∠BAO,∠GEA=∠GAE
∵EF⊥BC,
∴∠BFE=90°,
∴∠ABO+∠BEF=90°,
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF,
∴∠BAO+∠GAE=90°,
即AG与⊙O相切
(2)解:∵BC为直径,
∴∠BAC=90°,AC=6,AB=8,
∴BC=10,
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴ ![]() =
= ![]() =
= ![]()
∴EF=1.8,BF=2.4,
∴0F=0B﹣BF=5﹣2.4=2.6,
∴OE= ![]() =
= ![]()
【解析】(1)连接OA,由OA=OB,GA=GE得出∠ABO=∠BAO,∠GEA=∠GAE;再由EF⊥BC,得出∠BFE=90°,进一步由∠ABO+∠BEF=90°,∠BEF=∠GEA,最后得出∠GAO=90°求得答案;(2)BC为直径得出∠BAC=90°,利用勾股定理得出BC=10,由△BEF∽△BCA,求得EF、BF的长,进一步在△OEF中利用勾股定理得出OE的长即可.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目