题目内容
【题目】已知:如图,ABCD的两条对角线相交于点O,E是BO的中点.过点B作AC的平行线BF,交CE的延长线于点F,连接AF. 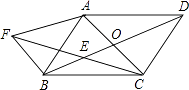
(1)求证:△FBE≌△COE;
(2)将ABCD添加一个条件,使四边形AFBO是菱形,并说明理由.
【答案】
(1)证明:如图,取BC的中点G,连接EG.
∵E是BO的中点,
∴EG是△BFC的中位线,
∴EG= ![]() BF.
BF.
同理,EG= ![]() OC,
OC,
∴BF=OC.
又∵四边形ABCD是平行四边形,
∴AO=CO,
∴BF=OC.
又∵BF∥AC,
∴∠FBE=∠COE.
在△FBE△COE中, 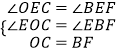 ,
,
∴△FBE≌△COE(AAS)
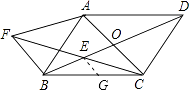
(2)解:当AC=BD时,四边形AFBO是菱形.理由如下:
∵AC=BD,
∴平行四边形ABCD是矩形,
∴OA=OC=OB=OD,
∴平行四边形AFBO是菱形.
【解析】(1)由AAS证得两个三角形全等即可.(2)当平行四边形ABCD的对角线相等,即平行四边形ABCD是矩形时,四边形AFBO是菱形.
【考点精析】根据题目的已知条件,利用平行四边形的性质和菱形的判定方法的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

【题目】某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.
时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
与此同时,该销售部还通过某网络电子商务平台销售鲜花,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 的函数关系如图所示.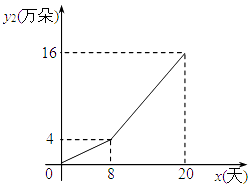
(1)求y1与x的二次函数关系式及自变量x的取值范围;
(2)求y2与x的函数关系式及自变量x的取值范围;
(3)当8≤x≤20时,设该花木公司鲜花日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时的最大值.