��Ŀ����
����Ŀ����ͼ��������y=��![]() +
+![]() +2��x���ཻ��A��B���㣬����A��B����ࣩ��y�ύ�ڵ�C��
+2��x���ཻ��A��B���㣬����A��B����ࣩ��y�ύ�ڵ�C��
��1����A��B�������꣮
��2������AC������P�ڵ�һ�����������ϣ�P�ĺ�����Ϊt���ı���ABPC�����ΪS�����ú�t��ʽ�ӱ�ʾS������tΪ��ֵʱ��S���

��3���ڣ�2���Ļ����ϣ��������������ϺͶԳ������Ƿ�ֱ���ڵ�G�͵�H��ʹ��A��G��H��P�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ���ֱ��д��G��H�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A����![]() ��0����B��2
��0����B��2![]() ��0������2����t=
��0������2����t=![]() ʱ��S���=4
ʱ��S���=4![]() ����3�����������ĵ�P������ΪG����
����3�����������ĵ�P������ΪG����![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G��
����G��![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G����
����G����![]() ��
��![]() ����H��
����H��![]() ��
��![]() ����
����
��������
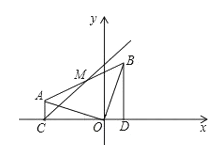
��1����y=0����![]() ���
���![]() ��
��![]() ���������A��B�������꣮
���������A��B�������꣮
��2����P��PQ��x����Q��P�ĺ�����Ϊt����P��t��p������![]() ��
��![]() ����S=S��AOC+S����OCPQ+S��PQB�г�S��t�ĺ�����ϵʽ�����ݶ��κ���������tΪ��ֵʱ��S���
����S=S��AOC+S����OCPQ+S��PQB�г�S��t�ĺ�����ϵʽ�����ݶ��κ���������tΪ��ֵʱ��S���
��3�������ߵĶԳ���Ϊ��![]() �ֱ�ʾ��ͼ������ƽ���ı��ε����ʼ������G��H������.
�ֱ�ʾ��ͼ������ƽ���ı��ε����ʼ������G��H������.
�⣺��1�������������![]() ��
��
��y=0����![]()
���![]() ��
��![]()
��![]()
��2�������������![]()
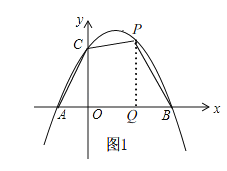
��x=0��
��y=2��
��C��0��2����
��ͼ1����P��PQ��x����Q��
��P�ĺ�����Ϊt��
����P��t��p����
��![]() ��
��![]()
��S=S��AOC+S����OCPQ+S��PQB
![]() ��
��
![]()
![]()
![]()
![]()
![]()
�൱![]() ʱ��S���
ʱ��S���![]()
��3�����������ĵ������ΪG����![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G��
����G��![]() ����
����![]() ����H��
����H��![]() ����
����![]() ����G����
����G����![]() ��
��![]() ����H��
����H��![]() ��
��![]() ����
����