题目内容
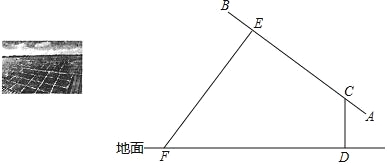
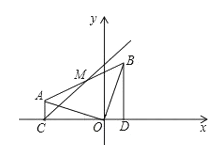
【题目】在平面直角坐标系中有一△BOD,![]() ,把 BO 绕点O 逆时针旋转 90°得OA, 连接AB,作
,把 BO 绕点O 逆时针旋转 90°得OA, 连接AB,作![]() 于点 C,点B 的坐标为(1,3).
于点 C,点B 的坐标为(1,3).
(1)求直线AB 的解析式;
(2)若AB 中点为 M,连接 CM,动点 P、Q 同时从 C 点出发,点 P 沿射线CM 以每秒2个单位长度的速度运动,点Q沿线段CD 以每秒1个单位长度的速度向终点 D 运动,当Q点运动到D 点时,P、Q同时停止运动,设△PQO 的面积为 S(![]() ),运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围;
),运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,是否存在这样的 P 点,使得P、O、B为顶点的三角形是直角三角形?若存在,求出对应的t 值和此时Q点的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
(3)存在这样的P点.
当∠POB为90°时,t=![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
当∠PBO为90°时,t=![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
当∠BPO为90°时,t=3,Q点坐标为(0,0)或t=2,Q点坐标为(-1,0)
【解析】
(1)根据待定系数法,先求出点A的坐标,然后将A、B两点坐标代入即可.(2)根据AB中点M,求出点M的坐标,在求出CM的解析式,过点P做PH垂直CO交CO于点H,用t表示出OQ和PH的长,根据![]() ,即可求出S关于t的函数关系式.(3)根据勾股定理,此题须分三种情况分别求t的值.
,即可求出S关于t的函数关系式.(3)根据勾股定理,此题须分三种情况分别求t的值.
解:(1)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设直线AB解析式为y=kx+b
将A、B两点坐标分别代入得:
![]()
解得:![]()
![]()
(2)∵![]() ,
,![]()
∴直线MC的解析式为![]()
![]()
过点P做![]() 交CO于点H,
交CO于点H,
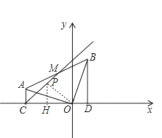
![]()
![]()
(3)∵直线MC的解析式为![]()
∴设P点坐标为(x,x+3),
①当∠POB为90°时
![]()
![]()
整理得:![]()
![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
此时t=![]() =
=![]()
②当∠PBO为90°时,
![]()
![]()
![]()
解得x=![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
此时t=![]()
③当∠BPO为90°时
![]()
![]()
整理得:![]()
![]() ,
,![]()
Q点坐标为(0,0)或(-1,0)
此时t=3+0=3或者t=3-1=2
故存在这样的P点.
当∠POB为90°时,t=![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
当∠PBO为90°时,t=![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
当∠BPO为90°时,t=3,Q点坐标为(0,0)或t=2,Q点坐标为(-1,0)

【题目】甲、乙两名同学的家与学校的距离均为![]() .甲同学先步行
.甲同学先步行![]() ,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的
,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的![]() 倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到![]() .
.
(1)解:设乙同学骑自行车的速度为![]() .完成表格:
.完成表格:
乙同学 | 甲同学 | ||
骑自行车 | 步行 | 乘公交车 | |
路程 |
|
| |
时间 |
| ||
(2)求乙同学骑自行车的速度.
(3)当甲同学到达学校时,乙同学离学校还有多少米?
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米) | 运费(元/吨·千米) | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水![]() 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?