题目内容
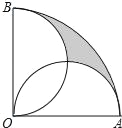
【题目】如图，在半径为2cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为_____．
【答案】
﹣1．
【解析】
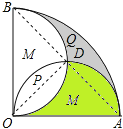
试题假设出扇形半径，再表示出半圆面积，以及扇形面积，进而即可表示出两部分P，Q面积相等．连接AB，OD，根据两半圆的直径相等可知∠AOD=∠BOD=45°，故可得出绿色部分的面积=S△AOD，利用阴影部分Q的面积为：S扇形AOB﹣S半圆﹣S绿色，故可得出结论．
解：∵扇形OAB的圆心角为90°，扇形半径为2，
∴扇形面积为：
=π（cm2），
半圆面积为：
×π×12=
（cm2），
∴SQ+SM =SM+SP=（cm2），
∴SQ=SP，
连接AB，OD，
∵两半圆的直径相等，
∴∠AOD=∠BOD=45°，
∴S绿色=S△AOD=
×2×1=1（cm2），
∴阴影部分Q的面积为：S扇形AOB﹣S半圆﹣S绿色=π﹣﹣1=﹣1（cm2）．
故答案为：﹣1．
练习册系列答案
名校课堂系列答案
相关题目
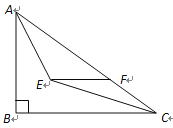
【题目】在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC于点F．
（1）求证：AC是⊙O的切线；
（2）若BF=6，⊙O的半径为5，求CE的长．
【题目】今年春北方严重干旱，某社区人畜饮水紧张，每天需从社区外调运饮用水120吨，有关部门紧急部署，从甲、乙两水厂调运饮用水到社区供水点，甲厂每天最多可调出80吨，乙厂每天最多可调出90吨，从两水厂运水到社区供水点的路程和运费如下表：
到社区供水点的路程（千米） | 运费（元/吨·千米） | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元，则从甲、乙两水厂各调运多少吨饮用水？
【2】设从甲厂调运饮用水
吨，总运费为W元，试写出W关于与的函数关系式，怎样安排调运方案才能使每天的总运费最省？
