Question

已知⊙O的半径为R，⊙P的半径为r（r＜R），且⊙P的圆心P在⊙O上．设C是⊙P上一点，过点C与⊙P相切的直线交⊙O于A、B两点．
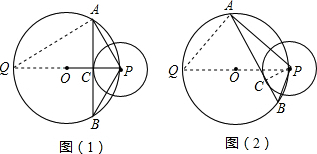
（1）若点C在线段OP上，（如图1）．求证：PA•PB=2Rr；
（2）若点C不在线段OP上，但在⊙O内部如图（2）．此时，（1）中的结论是否成立？若成立，请给予证明；若不成立，说明理由；
（3）若点C在⊙O的外部，如图（3）．此时，PA•PB与R，r的关系又如何？请直接写出，不要求给予证明或说明理由．

Answer 1

（1）证明：延长PO交⊙O于点Q，
连接AQ，如图（1），
∵AB与⊙P相切于点C，且PC是⊙P的半径，
∴AB⊥PC，即∠PCB=90°．
又∵PQ是⊙O的直径，
∴∠PAQ=90°．
∵∠PQA=∠PBC，
∴Rt△PAQ∽Rt△PCB，
∴

PA

PC

=

PQ

PB

，
即PA•PB=PQ•PC．
又∵PQ=2R，PC=r，
∴PA•PB=2Rr；

（2）（1）中的结论成立．
证明：连接PO并延长交⊙O于点Q，
连接AQ，PC，如图（2），
由已知条件，得
∠PAQ=∠PCB=90°．
又∠PQA=∠PBC，
∴Rt△PAQ∽Rt△PCB，
∴

PA

PC

=

PQ

PB

，
即PA•PB=PQ•PC=2Rr；

（3）PA•PB=2Rr．