题目内容
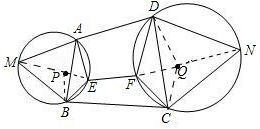
如图,四边形ABCD中,△ABM,△CDN是分别以AB、CD为一条边的正三角形,E、F分别在这二个三角形外接圆上,试问AE+EB+EF+FD+FC是否存在最小值?若存在最小值,则E、F两点的位置在什么地方?并说明理由.若不存在最小值,亦请说出理由.

如图,在两正三角形内作正△BEP、正△CFQ,连接PE、PM,QD,QN.
易证,△BPM≌△BEA,△CDF≌△CNQ,
∴PM=AE,QN=DF,
∴AE+EB+EF+FD+FC=MP+PE+EF+FQ+QN.
所以,AE+EB+EF+FD+FC存在最小值,即E、F两点位于MN与两圆的两个交点.
易证,△BPM≌△BEA,△CDF≌△CNQ,
∴PM=AE,QN=DF,
∴AE+EB+EF+FD+FC=MP+PE+EF+FQ+QN.
所以,AE+EB+EF+FD+FC存在最小值,即E、F两点位于MN与两圆的两个交点.


练习册系列答案
相关题目