题目内容
【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).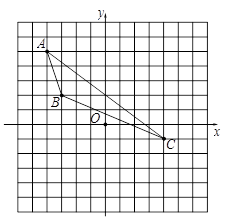
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高.
【答案】
(1)解: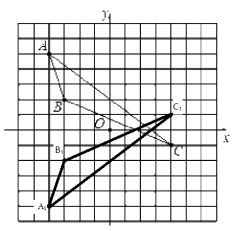 如图所示,△A1B1C1即为所求。
如图所示,△A1B1C1即为所求。
(2)解:A1(-4, -5),B1(﹣3,- 2),C1(4,1)
(3)解: 由图可得S△ABC=6×8×![]() -1×3×
-1×3×![]() -1×3-3×7×
-1×3-3×7×![]() =9
=9
又AC=![]() =10
=10
∵![]() AC×h=S△ABC
AC×h=S△ABC
∴h=9×2÷10=1.8
所以△ABC的AC边上的高为1.8![]()
【解析】(1)(2)中由关于X轴对称变换的性质易得A1(-4, -5),B1(﹣3,- 2),C1(4,1),在坐标系内,描点,连线即可。
可利用割补法计算出三角形ABC的面积,再利用勾股定理得AC的长,最后利用面积关系计算得到AC边上的高。
【考点精析】认真审题,首先需要了解坐标与图形变化-对称(关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目