ÌâÄżÄÚÈĘ
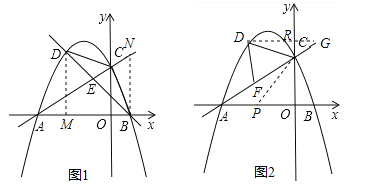
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÖ±Ïß![]() ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăCŁŹĆŚÎïÏß
ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăCŁŹĆŚÎïÏß![]() ŸčęAĄąCÁœ”㣏ÓëxÖá”ÄÁíÒ»œ»”ăÎȘ”ăBŁź
ŸčęAĄąCÁœ”㣏ÓëxÖá”ÄÁíÒ»œ»”ăÎȘ”ăBŁź
Łš1Ł©ÇóĆŚÎïÏß”ÄșŻÊę±íŽïÊœŁ»
Łš2Ł©”ăDÎȘÖ±ÏßACÉÏ·œĆŚÎïÏßÉÏÒ»¶Ż”㣻
ąÙÁŹœÓBCĄąCDŁŹÉèÖ±ÏßBDœ»Ï߶ÎACÓÚ”ăEŁŹĄśCDE”ÄĂæ»ęÎȘ![]() ŁŹĄśBCE”ÄĂæ»ęÎȘ
ŁŹĄśBCE”ÄĂæ»ęÎȘ![]() ŁŹÇó
ŁŹÇó![]() ”ÄŚîŽóÖ”Ł»
”ÄŚîŽóÖ”Ł»
ąÚčę”ăDŚśDFĄÍACŁŹŽčŚăÎȘ”ăFŁŹÁŹœÓCDŁŹÊÇ·ńŽæÔÚ”ăDŁŹÊč”ĂĄśCDFÖĐ”ÄÄłžöœÇÇĄșĂ”ÈÓÚĄÏBAC”Ä2±¶ŁżÈôŽæÔÚŁŹÇó”ăD”ÄșáŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź

ĄŸŽđ°žĄżŁš1Ł©![]() Ł»Łš2Ł©ąÙ
Ł»Łš2Ł©ąÙ![]() Ł»ąÚ©2»ò
Ł»ąÚ©2»ò![]() Łź
Łź
ĄŸœâÎöĄż
ÊÔÌâ·ÖÎöŁșŁš1Ł©žùŸĘÌâÒâ”Ă”œAŁš©4ŁŹ0Ł©ŁŹCŁš0ŁŹ2Ł©ŽúÈë![]() ŁŹÓÚÊǔÔœœáÂÛŁ»
ŁŹÓÚÊǔÔœœáÂÛŁ»
Łš2Ł©ąÙÈçÍŒŁŹÁîy=0ŁŹœâ·œłÌ”Ă”œx1=©4ŁŹx2=1ŁŹÇó”ĂBŁš1ŁŹ0Ł©ŁŹčęDŚśDMĄÍxÖáÓÚMŁŹčęBŚśBNĄÍxÖ᜻ÓÚACÓÚNŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊŒŽżÉ”Ă”œœáÂÛŁ»
ąÚžùŸĘčŽčɶšÀí”ÄÄ涚Àí”Ă”œĄśABCÊÇÒÔĄÏACBÎȘÖ±œÇ”ÄÖ±œÇÈęœÇĐÎŁŹÈĄAB”ÄÖĐ”ăPŁŹÇó”ĂPŁš![]() ŁŹ0Ł©ŁŹ”Ă”œPA=PC=PB=
ŁŹ0Ł©ŁŹ”Ă”œPA=PC=PB=![]() ŁŹčꌜxÖá”ÄÆœĐĐÏßœ»yÖáÓÚRŁŹœ»AC”ÄŃÓÏßÓÚGŁŹÇéżöÒ»ŁșÈçÍŒŁŹĄÏDCF=2ĄÏBAC=ĄÏDGC+ĄÏCDGŁŹÇéżö¶țŁŹĄÏFDC=2ĄÏBACŁŹœâÖ±œÇÈęœÇĐÎŒŽżÉ”Ă”œœáÂÛŁź
ŁŹčꌜxÖá”ÄÆœĐĐÏßœ»yÖáÓÚRŁŹœ»AC”ÄŃÓÏßÓÚGŁŹÇéżöÒ»ŁșÈçÍŒŁŹĄÏDCF=2ĄÏBAC=ĄÏDGC+ĄÏCDGŁŹÇéżö¶țŁŹĄÏFDC=2ĄÏBACŁŹœâÖ±œÇÈęœÇĐÎŒŽżÉ”Ă”œœáÂÛŁź
ÊÔÌâœâÎöŁșŁš1Ł©žùŸĘÌâÒâ”ĂAŁš©4ŁŹ0Ł©ŁŹCŁš0ŁŹ2Ł©ŁŹĄßĆŚÎïÏß![]() ŸčęAĄąCÁœ”㣏Ąà
ŸčęAĄąCÁœ”㣏Ąà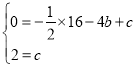 ŁŹĄà
ŁŹĄà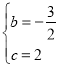 ŁŹĄà
ŁŹĄà![]() Ł»
Ł»
Łš2Ł©ąÙÈçÍŒŁŹÁîy=0ŁŹĄà![]() ŁŹĄàx1=©4ŁŹx2=1ŁŹĄàBŁš1ŁŹ0Ł©ŁŹčęDŚśDMĄÍxÖáÓÚMŁŹčęBŚśBNĄÍxÖ᜻ÓÚACÓÚNŁŹĄàDMĄÎBNŁŹĄàĄśDMEĄŚĄśBNEŁŹĄà
ŁŹĄàx1=©4ŁŹx2=1ŁŹĄàBŁš1ŁŹ0Ł©ŁŹčęDŚśDMĄÍxÖáÓÚMŁŹčęBŚśBNĄÍxÖ᜻ÓÚACÓÚNŁŹĄàDMĄÎBNŁŹĄàĄśDMEĄŚĄśBNEŁŹĄà![]() =
=![]() =
=![]() ŁŹÉèDŁšaŁŹ
ŁŹÉèDŁšaŁŹ ![]() Ł©ŁŹĄàMŁšaŁŹ
Ł©ŁŹĄàMŁšaŁŹ![]() Ł©ŁŹĄßBŁš1.0Ł©ŁŹĄàNŁš1ŁŹ
Ł©ŁŹĄßBŁš1.0Ł©ŁŹĄàNŁš1ŁŹ![]() Ł©ŁŹĄà
Ł©ŁŹĄà![]() =
=![]() =
=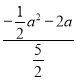 =
=![]() Ł»Ąà”±a=-2ʱŁŹ
Ł»Ąà”±a=-2ʱŁŹ![]() ”ÄŚîŽóÖ”ÊÇ
”ÄŚîŽóÖ”ÊÇ![]() Ł»
Ł»
ąÚĄßAŁš©4ŁŹ0Ł©ŁŹBŁš1ŁŹ0Ł©ŁŹCŁš0ŁŹ2Ł©ŁŹĄàAC=![]() ŁŹBC=
ŁŹBC=![]() ŁŹAB=5ŁŹĄàAC2+BC2=AB2ŁŹĄàĄśABCÊÇÒÔĄÏACBÎȘÖ±œÇ”ÄÖ±œÇÈęœÇĐÎŁŹÈĄAB”ÄÖĐ”ăPŁŹĄàPŁš
ŁŹAB=5ŁŹĄàAC2+BC2=AB2ŁŹĄàĄśABCÊÇÒÔĄÏACBÎȘÖ±œÇ”ÄÖ±œÇÈęœÇĐÎŁŹÈĄAB”ÄÖĐ”ăPŁŹĄàPŁš![]() ŁŹ0Ł©ŁŹĄàPA=PC=PB=
ŁŹ0Ł©ŁŹĄàPA=PC=PB=![]() ŁŹĄàĄÏCPO=2ĄÏBACŁŹĄàtanĄÏCPO=tanŁš2ĄÏBACŁ©=
ŁŹĄàĄÏCPO=2ĄÏBACŁŹĄàtanĄÏCPO=tanŁš2ĄÏBACŁ©=![]() ŁŹčꌜxÖá”ÄÆœĐĐÏßœ»yÖáÓÚRŁŹœ»AC”ÄŃÓł€ÏßÓÚGŁź·ÖÁœÖÖÇéżöŁș
ŁŹčꌜxÖá”ÄÆœĐĐÏßœ»yÖáÓÚRŁŹœ»AC”ÄŃÓł€ÏßÓÚGŁź·ÖÁœÖÖÇéżöŁș
ÇéżöÒ»ŁșÈçÍŒŁŹĄàĄÏDCF=2ĄÏBAC=ĄÏDGC+ĄÏCDGŁŹĄàĄÏCDG=ĄÏBACŁŹĄàtanĄÏCDG=tanĄÏBAC=![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹÁîDŁšaŁŹ
ŁŹÁîDŁšaŁŹ![]() Ł©ŁŹĄàDR=©aŁŹRC=
Ł©ŁŹĄàDR=©aŁŹRC=![]() ŁŹĄà
ŁŹĄà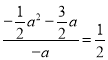 ŁŹĄàa1=0ŁšÉáÈ„Ł©ŁŹa2=©2ŁŹĄàxD=©2Łź
ŁŹĄàa1=0ŁšÉáÈ„Ł©ŁŹa2=©2ŁŹĄàxD=©2Łź
Çéżö¶țŁŹĄàĄÏFDC=2ĄÏBACŁŹĄàtanĄÏFDC=![]() ŁŹÉèFC=4kŁŹĄàDF=3kŁŹDC=5kŁŹĄßtanĄÏDGC=
ŁŹÉèFC=4kŁŹĄàDF=3kŁŹDC=5kŁŹĄßtanĄÏDGC=![]() =
=![]() ŁŹĄàFG=6kŁŹĄàCG=2kŁŹDG=
ŁŹĄàFG=6kŁŹĄàCG=2kŁŹDG=![]() kŁŹĄà
kŁŹĄà
ĄàRC=![]() kŁŹRG=
kŁŹRG=![]() kŁŹDR=
kŁŹDR=![]() k©
k©![]() k=
k=![]() kŁŹĄà
kŁŹĄà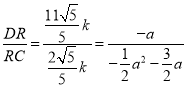 ŁŹĄàa1=0ŁšÉáÈ„Ł©ŁŹa2=
ŁŹĄàa1=0ŁšÉáÈ„Ł©ŁŹa2=![]() Łź
Łź
ŚÛÉÏËùÊöŁș”ăD”ÄșáŚű±êÎȘ©2»ò![]() Łź
Łź

ĄŸÌâÄżĄżÒŃÖȘyÊÇx ”ÄșŻÊ꣏ŚÔ±äÁżx”ÄÈĄÖ”·¶Î§ÊÇx >0ŁŹÏ±íÊÇyÓëx ”ÄŒžŚé¶ÔÓŠÖ”.
x | Ą€Ą€Ą€ | 1 | 2 | 3 | 5 | 7 | 9 | Ą€Ą€Ą€ |
y | Ą€Ą€Ą€ | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | Ą€Ą€Ą€ |
ĐĄÌÚžùŸĘŃ§Ï°Ò»ŽÎșŻÊę”ÄŸŃ飏ÀûÓĂÉÏÊö±ížńËù·ŽÓłłö”ÄyÓëxÖźŒä”ı仯čæÂÉŁŹ¶ÔžĂșŻÊę”ÄÍŒÏóÓëĐÔÖÊœűĐĐÁËÌœŸż.
ÏÂĂæÊÇĐĄÌÚ”ÄÌœŸżčęłÌŁŹÇëČčłäÍêŐûŁș
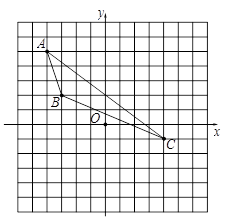
Łš1Ł©ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ” ![]() ÖĐŁŹĂèłöÁËÒÔÉϱíÖĐžś¶Ô¶ÔÓŠÖ”ÎȘŚű±ê”Ä”ă.žùŸĘĂèłö”Ĕ㣏»łöžĂșŻÊę”ÄÍŒÏó;
ÖĐŁŹĂèłöÁËÒÔÉϱíÖĐžś¶Ô¶ÔÓŠÖ”ÎȘŚű±ê”Ä”ă.žùŸĘĂèłö”Ĕ㣏»łöžĂșŻÊę”ÄÍŒÏó;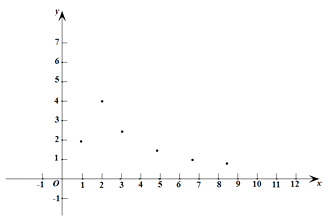
Łš2Ł©žùŸĘ»łö”ÄșŻÊęÍŒÏóŁŹĐŽłöŁș
ąÙx=4¶ÔÓŠ”ÄșŻÊęÖ”yÔŒÎȘŁ»
ąÚžĂșŻÊę”ÄÒ»ÌőĐÔÖÊŁș Łź