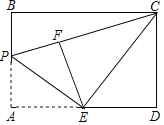
题目内容
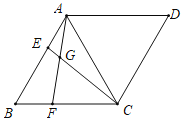
【题目】定义:若一个三角形一条边上的高长为这条边长的一半,则称该三角形为这条边上的“半高”三角形,这条高称为这条边上的“半高”,如图,△ABC是BC边上的“半高”三角形.点P在边AB上,PQ∥BC交AC于点Q,PM⊥BC于点M,QN⊥BC于点N,连接MQ.
(1)请证明△APQ为PQ边上的“半高”三角形.
(2)请探究BM,PM,CN之间的等量关系,并说明理由;
(3)若△ABC的面积等于16,求MQ的最小值
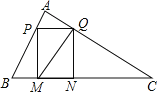
【答案】(1)见解析;(2)2PM=BM+CN,理由见解析;(3)![]() .
.
【解析】
(1)根据平行相似,证明△APQ∽△ABC,利用相似三角形对应边的比等于对应高的比:![]() ,由“半高”三角形的定义可结论;
,由“半高”三角形的定义可结论;
(2)证明四边形PMNQ是矩形,得PQ=MN,PM=KR,代入AR=![]() BC,可得结论;
BC,可得结论;
(3)先根据△ABC的面积等于16,计算BC和AR的长,设MN=x,则BM+CN=8﹣x,PM=QN=![]() (8﹣x),根据勾股定理表示MQ,配方可得最小值.
(8﹣x),根据勾股定理表示MQ,配方可得最小值.
(1)证明:如图,过A作AR⊥BC于R,交PQ于K,
∵△ABC是BC边上的“半高”三角形,
∴AR=![]() BC,
BC,
∵PQ∥BC,
∴△APQ∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AK=![]() PQ,
PQ,
∴△APQ为PQ边上的“半高”三角形.
(2)解:2PM=BM+CN,理由是:
∵PM⊥BC,QN⊥BC,
∴∠PMN=∠MNQ=∠MPQ=90°,
∴四边形PMNQ是矩形,
∴PQ=MN,PM=KR,
∵AK=![]() PQ,AR=
PQ,AR=![]() BC,
BC,
∴AK+RK=![]() (BM+MN+CN),
(BM+MN+CN),
![]() PQ+PM=
PQ+PM=![]() BM+
BM+![]() MN+
MN+![]() CN,
CN,
∴2PM=BM+CN;
(3)解:∵△ABC的面积等于16,
∴![]() =16,
=16,
∵AR=![]() BC,
BC,
![]() =16,
=16,
BC=8,AR=4,
设MN=x,则BM+CN=8﹣x,PM=QN=![]() (8﹣x),
(8﹣x),
∵MQ=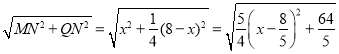 ,
,
∴当x=![]() 时,MQ有最小值是
时,MQ有最小值是![]() .
.

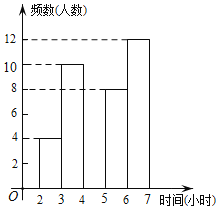
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?