Question

【题目】发现

如图1，在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中（n为大于3的整数），∠A1A2A3＝∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣（n﹣4）×180°．

验证

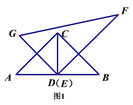
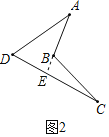
（1）如图2，在有一个“凹角∠ABC”的四边形ABCD中，证明：∠ABC＝∠A+∠C+∠D．

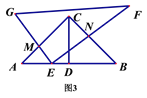
（2）证明3，在有一个“凹角∠ABC”的六边形ABCDEF中，证明；∠ABC＝∠A+∠C+∠D+∠E+∠F﹣360°．

延伸

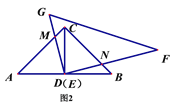
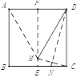
（3）如图4，在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中（n为大于4的整数），∠A1A2A3+∠A2A3A4＝∠A1+∠A4+∠A5+∠A6……+∠An﹣（n﹣　 ）×180°．

Answer 1

【答案】（1）见解析；（2）见解析；（3）6．

【解析】

（1）如图2，延长AB交CD于E，可知∠ABC＝∠BEC+∠C，∠BEC＝∠A+∠D，即可解答

（2）如图3，延长AB交CD于G，可知∠ABC＝∠BGC+∠C，即可解答

（3）如图4，延长A2A3交A5A4于C，延长A3A2交A1An于B，可知∠A1A2A3+∠A2A3A4＝∠A1+∠2+∠A4+∠4，再找出规律即可解答

（1）如图2，延长AB交CD于E，

则∠ABC＝∠BEC+∠C，∠BEC＝∠A+∠D，

∴∠ABC＝∠A+∠C+∠D；

（2）如图3，延长AB交CD于G，则∠ABC＝∠BGC+∠C，

∵∠BGC＝180°﹣∠BGC，∠BGD＝3×180°﹣（∠A+∠D+∠E+∠F），

∴∠ABC＝∠A+∠C+∠D+∠E+∠F﹣360°；

（3）如图4，延长A2A3交A5A4于C，延长A3A2交A1An于B，

则∠A1A2A3+∠A2A3A4＝∠A1+∠2+∠A4+∠4，

∵∠1+∠3＝（n﹣2﹣2）×180°﹣（∠A5+∠A6……+∠An），

而∠2+∠4＝360°﹣（∠1+∠3）＝360°﹣[（n﹣2﹣2）×180°﹣（∠A5+∠A6……+∠An）]，

∴∠A1A2A3+∠A2A3A4＝∠A1+∠A4+∠A5+∠A6……+∠An﹣（n﹣6）×180°．

故答案为：6．