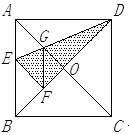题目内容
如图,在菱形ABCD中,∠C=60°,AB=4,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=60°.
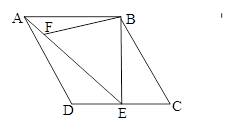
(1)求证:△ABF∽△EAD;
(2)求BF的长.

(1)求证:△ABF∽△EAD;
(2)求BF的长.
(1)因为四边形ABCD为菱形,∠C=60°,所以∠D=120°
因为∠BFE=60°所以∠BFA=∠D=120°
因为AB∥DC,所以∠BAF=∠AED,
所以△ABF∽△EAD;……………4分
(2):∵BE⊥CD,
∴△BEC为Rt△.
∵AB=BC=4,∠C=60°,
∴EC=2
BE=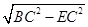 =
=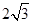
:∵BE⊥CD,AB∥DC,
∴EB⊥AB.
∴△ABE为Rt△.
AE=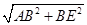 =
=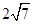
∵△ABF∽△EAD,
∴AB /AE ="BF/" AD .
∴BF=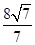 …………………8分
…………………8分
因为∠BFE=60°所以∠BFA=∠D=120°
因为AB∥DC,所以∠BAF=∠AED,
所以△ABF∽△EAD;……………4分
(2):∵BE⊥CD,
∴△BEC为Rt△.
∵AB=BC=4,∠C=60°,
∴EC=2
BE=
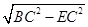 =
=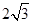
:∵BE⊥CD,AB∥DC,
∴EB⊥AB.
∴△ABE为Rt△.
AE=
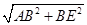 =
=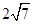
∵△ABF∽△EAD,
∴AB /AE ="BF/" AD .
∴BF=
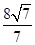 …………………8分
…………………8分根据菱形的性质及相似三角形的判定方法得到△ABF∽△EAD,再根据相似三角形的边对应成比例即可求得BF的长

练习册系列答案
相关题目
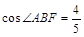 ,求BC的长.
,求BC的长.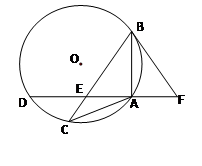
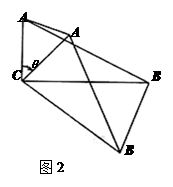
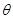 (0°<
(0°<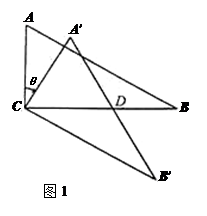
 中,点
中,点 分别在边
分别在边 上,BE⊥EF,
上,BE⊥EF,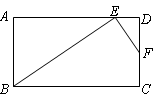
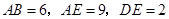 ,求CF的长.
,求CF的长.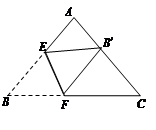
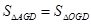 ;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )
;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )