Question

【题目】如图，A、B是圆O上的两点，∠AOB=120°，C是AB弧的中点．

（1）求证：AB平分∠OAC；
（2）延长OA至P使得OA=AP，连接PC，若圆O的半径R=1，求PC的长．

Answer 1

【答案】
（1）

证明：连接OC，

∵∠AOB=120°，C是AB弧的中点，

∴∠AOC=∠BOC=60°，

∵OA=OC，

∴△ACO是等边三角形，

∴OA=AC，同理OB=BC，

∴OA=AC=BC=OB，

∴四边形AOBC是菱形，

∴AB平分∠OAC

（2）

解：连接OC，

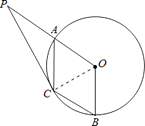
∵C为弧AB中点，∠AOB=120°，

∴∠AOC=60°，

∵OA=OC，

∴OAC是等边三角形，

又∵OA=AP，

∴AP=AC，

∴∠APC=30°，

∴△OPC是直角三角形，

∴ ．

【解析】（1）连接OC，由∠AOB=120°，C是AB弧的中点，∠AOC=∠BOC=60°，即可证明△ACO是等边三角形，同理可证△BCO是等边三角形，即OA=OB=AC=BC，则四边形AOBC是菱形，根据菱形的对角线平分一组对角，可得AB平分∠OAC；
（2）证△OPC是直角三角形即可求得.