题目内容
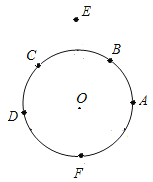
【题目】已知![]() 如图所示,点
如图所示,点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离均等于
三点的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() . 射线
. 射线![]() 与射线
与射线![]() 关于
关于![]() 对称,过点 C作
对称,过点 C作![]() 于
于![]() .
.
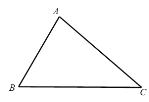
(1)依题意补全图形(保留作图痕迹);
(2)判断直线![]() 与图形
与图形![]() 的公共点个数并加以证明.
的公共点个数并加以证明.
【答案】(1)补全图形见解析;(2)直线![]() 与图形
与图形![]() 有一个公共点,证明见解析.
有一个公共点,证明见解析.
【解析】
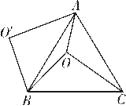
(1)根据题意可知,点O为△ABC的外心,作AC、BC的垂直平分线,交点为O,然后做出圆O,AC为∠OAM的角平分线,过C作![]() 于F,即可得到图形;
于F,即可得到图形;
(2)连接OC,由AC平分∠OAM,则![]() ,然后证明
,然后证明![]() ,由
,由![]() ,得到
,得到![]() ,得到CF是圆O的切线,即可得到结论.
,得到CF是圆O的切线,即可得到结论.
解:(1)依题意补全图形,如图,
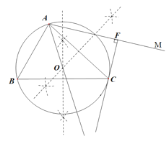
(2)如图,直线![]() 与图形
与图形![]() 有一个公共点
有一个公共点
证明:连接![]() ,
,
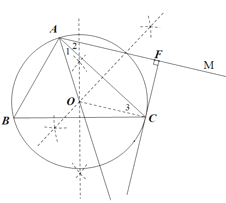
∵射线![]() 与射线
与射线![]() 关于
关于![]() 对称,
对称,
∴AC平分∠OAM,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 于
于![]()
∴![]() ,
,
∵图形![]() 即⊙
即⊙![]() ,
,![]() 为半径,
为半径,
∴![]() 与⊙O相切,即
与⊙O相切,即![]() 与图形
与图形![]() 有一个公共点.
有一个公共点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目