题目内容
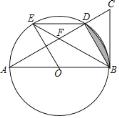
【题目】如图,已知![]() 的半径为1,按如下步骤作图:
的半径为1,按如下步骤作图:
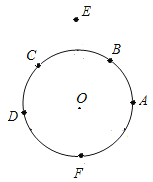
①以![]() 上的点A为圆心,1为半径画弧交
上的点A为圆心,1为半径画弧交![]() 于点B;
于点B;
②依次在![]() 上取点C和D,使得
上取点C和D,使得![]() ;
;
③分别以点A和D为圆心,AC长为半径画弧交于点E;
④以点A为圆心,OE长为半径画弧交![]() 于点F.
于点F.
则以下说法不正确的是( )
A.AC=![]() B.AF
B.AF![]() C.∠ACF=45°D.∠BEO=30°
C.∠ACF=45°D.∠BEO=30°
【答案】D
【解析】
连接OB、AD、AE、DE、AC、OE、AF、DF、CF,BE,连接AB并延长交OE的延长线于H点,根据作图过程可得三角形ADC为直角三角形,AD为直径,根据弧与圆周角的关系及解直角三角形即可求解.
如图所示:连接OB、AD、AE、DE、AC、OE、AF、DF、CF,连接AB并延长交OE的延长线于H点,连接BE,
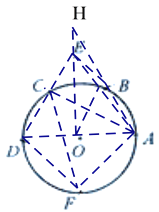
根据作法①可得:△ABO为等边三角形,
∴∠AOB=∠OAB=60°
∵![]()
∴∠DAC=30°,∠AOD=180°,AD为直径
∴CD=![]() ,AC=
,AC=![]() ,故A正确;
,故A正确;
由③得:AE=ED=AC=![]()
∴EO⊥AD
∴![]()
∴AF=EO=![]() ,故B正确;
,故B正确;
∵∠AFD=90°
∴![]()
∴∠ACD=∠ADF=45°,故C正确;
∵![]()
∴∠BAO>∠EAO
连接AB并延长交OE的延长线于H点,
则∠H=30°,∠BEO>30°,故D错误.
故选:D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目