Question

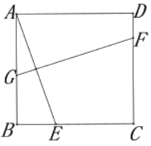
【题目】如图，在□ABCD中，AB＝26，AD＝6，将□ABCD绕点A旋转，当点D的对应点D′落在AB边上时，点C的对应点C′恰好与点B、C在同一直线上，则此时△C′D′B的面积为（）

A.120B.240C.260D.480

Answer 1

【答案】B

【解析】

根据平行四边形的性质和旋转的性质可推出∠C′BD′=∠C=∠D′AB′=∠BD′C′，因此可得△C′BD′为等腰三角形，进而可推出△C′BD′的高，即可算出面积．

如图：

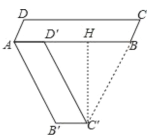
∵□ABCD中绕点A旋转后得到□AB′C′D′，

∴∠DAB=∠D′AB′，AB=AB′=C′D′=26，

∵AB′∥C′D′，

∴∠D′AB′=∠BD′C′，

∵四边形ABCD为平行四边形，

∴∠C=∠DAB，

∴∠C=∠BD′C′，

∵点C′、B、C在一条直线上，而AB//CD，

∴∠C=∠C′BD′，

∴∠C′BD′=∠BD′C′

∴△C′BD′为等腰三角形，

作C′H⊥D′B，则BH=D′H，

∵AB=26，AD=6，

∴BD′=20，

∴D′H=10，

∴C′H=，

∴△C′D′B的面积=·BD′·C′H=×20×24=240，

故选：B．